
за кілька хвилин до закінчення матчу. Але, розгубивши в кінцівці все перевага, вже поступалася одне очко 49:50. Далі сталося неймовірне! Іван Едешко кидає м'яч через лицьової лінії через весь майданчик під кільце американців, де наш центровий Олександр Бєлов приймає м'яч в оточенні двох суперників і вкладає його в кошик. 51:50 - ми олімпійські чемпіони.
Американці тоді не визнали поразки і відмовилися від отримання срібних медалей. Чи можливо за три секунди зробити те, що зробили наші гравці? Згадаймо фізику!
У цій статті ми розглянемо рух тіла, кинутого під кутом до горизонту, складемо в Excel програму вирішення цього завдання при різних поєднаннях вихідних даних і спробуємо відповісти на поставлене вище питання.
Це досить широко відома задача в фізиці. У нашому випадку тіло, кинуте під кутом до горизонту - це баскетбольний м'яч. Ми розрахуємо початкову швидкість, час і траєкторію польоту м'яча, кинутого через весь майданчик Іваном Едешко і потрапив в руки Олександра Бєлова.
Математика і фізика польоту баскетбольного м'яча.
Представлені нижче формули і розрахунок вexcelявляются універсальними для широкого кола завдань про тілах, кинутих під кутом до горизонту і летять по параболічної траєкторії без урахування впливу тертя об повітря.
Розрахункова схема представлена на малюнку, розташованому нижче. Запускаємо програму MS Excel або OOo Calc.
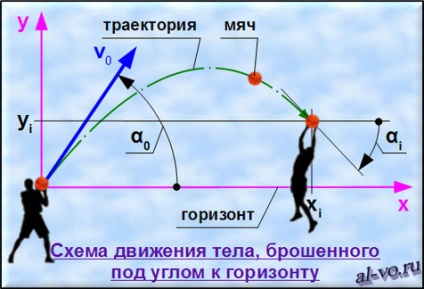
Початкові дані:
1. Так як ми знаходимося на планеті Земля і розглядаємо балістичну завдання - рух тіл в полі тяжіння Землі, то першим ділом запишемо основну характеристику гравітаційного поля - прискорення вільного падіння g в м / с 2
в клітинку D3: 9,81
2. Розміри баскетбольного майданчика - 28 метрів довжина і 15 метрів ширина. Відстань польоту м'яча майже через весь майданчик до кільця від протилежної лицьової лінії по горизонталі x в метрах впишемо
в клітинку D4: 27,000
3. Якщо прийняти, що кидок Едешко зробив з висоти близько двох метрів, а Бєлов зловив м'яч якраз десь на рівні кільця, то при висоті баскетбольного кільця 3,05 метра відстань між точками вильоту і прильоту м'яча складе по вертикалі 1 метр. Запишемо вертикальне переміщення y в метрах
в клітинку D5: 1,000
в комірку D6: 20,000
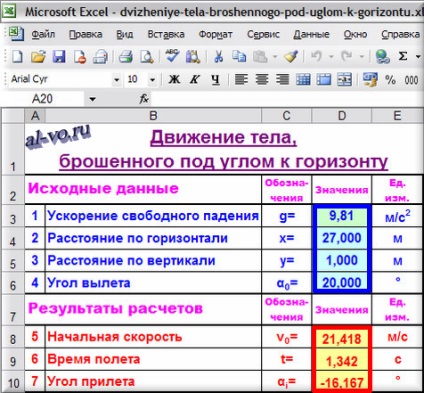
Результати розрахунків:
Основні рівняння, що описують рух тіла, кинутого під кутом до горизонту без урахування опору повітря:
5. Висловимо час t з першого рівняння, підставимо в друге і обчислимо початкову швидкість польоту м'яча v0 в м / с
в осередку D8: = (D3 * D4 ^ 2/2 / COS (РАДІАНИ (D6)) ^ 2 / (D4 * TAN (РАДІАНИ (D6)) -D5)) ^ 0,5 = 21,418
6. Час польоту м'яча від рук Едешко до рук Бєлова t в секундах розрахуємо, знаючи тепер v0, з першого рівняння
в осередку D9: = D4 / D8 / COS (РАДІАНИ (D6)) = 1,342
7. Знайдемо кут напрямку швидкості польоту м'яча αi в цікавій для нас точці траєкторії. Для цього вихідну пару рівнянь запишемо в наступному вигляді:
Це рівняння параболи - траєкторії польоту.
Нам необхідно знайти кут нахилу дотичній до параболи в цікавій для нас точці - це і буде кут αi. Для цього візьмемо похідну, яка представляє собою тангенс кута нахилу дотичної:
Розрахуємо кут прильоту м'яча в руки Бєлова αi в градусах
в осередку D10: = ATAN (TAN (РАДІАНИ (D6)) -D3 * D4 / D8 ^ 2 / COS (РАДІАНИ (D6)) ^ 2) / ПІ () * 180 = -16,167
Розрахунок в excel, в принципі, закінчений.
Інші варіанти розрахунків:
Використовуючи написану програму, можна швидко і просто при інших поєднаннях вихідних даних зробити обчислення.
Нехай, дані горизонтальна x = 27 метрів, вертикальна y = 1 метр дальності польоту і початкова швидкість v0 = 25 м / с.
Потрібно знайти час польоту t і кути вильоту α0 і прильоту αi
Встановлюємо в осередку D8 значення 25,000 за рахунок зміни підбором значення в комірці D6. Результат на малюнку внизу.
Вихідні дані в цьому варіанті розрахунку в excel (як, втім, і в попередньому) виділені синіми рамками, а результати обведені червоними прямокутними рамками!
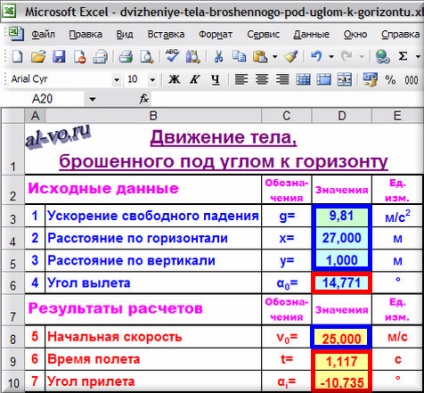
Встановлюючи в табліцеExcelнекоторое цікавить значення в одній з комірок зі світло-жовтою заливкою за рахунок підбору зміненого значення в одній з комірок зі світло-бірюзовою заливкою, можна отримати в загальному випадку десять різних варіантів рішення задачі про рух тіла, кинутого під кутом до горизонту при десяти різних наборах вихідних даних.