Інтегрування тригонометричних функцій за допомогою універсальної тригонометричної підстановки.
Розглянемо деякі випадки знаходження інтеграла від тригонометричних функцій. Функцію зі змінними sin x і cos x, над якими виконуються раціональні дії (додавання, віднімання, множення і ділення) прийнято позначати R (sin x; cos x), де R - знак раціональної функції.
Обчислення невизначених інтегралів тіпасводітся до обчислення інтегралів від paціoнaльнoй фyнкціі підстановкою. яка називається універсальною.
,
де R1 (t) - раціональна функція від t. Зазвичай цей спосіб досить громіздкий, зате він завжди призводить до результату.
На практиці застосовують і інші, більш прості підстановки, в залежності від властивостей (і виду) підінтегральної фyнкціі. У частнocті, зручні наступні правила:
1) якщо функція R (sinx; cos x) непарна відносно sinx, тобто R (- sinx; cos x) = - R (sin x; cos x), то підстановка cosx = t раціоналізує інтеграл;
2) якщо функція R (sinx; cos x) непарна відносно cosx, тобто R (sinx; - cosx) = - R (sinx; cosx), то робиться підстановка sinx = t;
3) якщо функція R (sin x; cos x) парна щодо sinx і cosx R (- sin x; - cos x) = R (sin x; cos x), то інтеграл раціоналізується підстановкою tgx = t. Така ж підстановка застосовується, якщо інтеграл має вигляд
Приклад Знайти інтеграл
Рішення: Зробити універсальну підстановку Тоді dx =,,. отже,
Деякі особливі тригонометричні підстановки.
Інтеграли типу ∫sinmх • cosnx dx
Для знаходження таких інтегралів використовуються наступні прийоми:
1) підстановка sinx = t, якщо n - ціле позитивне непарне число;
2) підстановка cosx = t, якщо m - ціле позитивне непарне число;
3) формули пониження порядку: cos 2 x = 1/2 (1 + cos2x), sin 2 x = 1/2 (1-cos 2x), sinx-cosx = 1/2 sin2x, якщо тип - цілі невід'ємні парні числа;
4) підстановка tg х = t, якщо m + n - є парне негативне ціле число.
Приклад Знайти інтеграл
Рішення: Застосуємо підстановку sinx = t. Тоді х = arcsint, dx І
Використання тригонометричних перетворень
Інтеграли типу обчислюються за допомогою відомих формул тригонометрії:
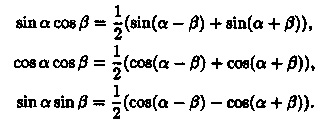
Приклад Знайти інтеграл
Інтегрування ірраціональних виразів.
Розглянемо деякі типи інтегралів, що містять ірраціональні функції.
Інтеграли типу називають невизначеними інтегралами від квадратичних иррациональностей. Їх можна знайти наступним обpaзoм:
під радикалом виділити повний квадрат
і зробити підстановку х + b / 2a = t. При цьому перші два інтеграла наводяться до табличних, а третій - до суми двох табличних інтегралів.
Приклад Знайти інтеграли
Рішення: Так як,
Cдeлаем підстановку x + 1/4 = t, x = t-1/4, dx = dt. тоді
Інтеграли типу, де Рn (х) - многочлен ступеня n, можна обчислювати, користуючись формулою
де Qn-1 (x) - многочлен ступеня n-1 з неопpедeлeннимі коефіцієнтами, - також невизначений коефіцієнт.
Всі невизначені коефіцієнти знаходяться з тотожності, одержуваного дифференцированием обох частин рівності (1):
після чого необхідно прирівняти коефіцієнти при однакових ступенях невідомої х.
Приклад Знайти інтеграл
Рішення: За формулою (1) маємо:
Диференціюючи це рівність, отримуємо:
Порівнюємо коефіцієнти при однакових степенях х:
Звідси А = -1 / 2, B = 3/2, = 2. отже,
Інтеграли типу де а, b, с, d - дійсні числа, , . , - натуральні числа, зводяться до інтегралів від раціональної функції шляхом підстановки де К - найменше общee кратне знаменників дробів
Дійсно, з підстановки слід, що і
т. е. х і dx виражаються через раціональні функції від t. При цьому і кожна ступінь дробу виражається через раціональну функцію від t.
Приклад Знайти інтеграл
Рішення: Найменша общee кратне знаменників дробів 2/3 і 1/2 є 6.
Тому вважаємо х + 2 = t 6. х = t 6 -2, dx = 6t 5 dt, Отже,
ПрімерУказать підстановку для знаходження інтегралів:
Рішення: Для I1 підстановка х = t 2. для I2 підстановка
Інтеграли типу приводяться до интегралам від функцій, раціонально залежать від тригонометричних функцій, за допомогою наступних тригонометричних підстановок: х = а • sint для першого інтеграла; х = а • tgt для другого інтеграла; для третього інтеграла.
Тут підінтегральна функція є раціональна функція відносно х іВиделів під радикалом повний квадрат і зробивши підстановку, інтеграли вказаного типу приводяться до интегралам вже pасcмoтpeннoгo типу, т. Е. До інтегралів типу Ці інтеграли можна обчислити за допомогою відповідних тригонометричних підстановок.
Приклад Знайти інтеграл
Рішення: Так як х 2 + 2х-4 = (х + 1) 2 -5, то х + 1 = t, x = t-1, dx = dt. ПоетомуПоложім

Зауваження: Інтеграл типу целессooбразно знаходити за допомогою підстановки х = 1 / t.
Інтегрування диференціального бінома
Інтеграли типу (звані інтегралами від диференціального бінома), де а, b - дійсні числа; m, n, р - раціональні числа, беруться лише в разі, коли хоча б одне з чисел р, (m + 1) / n або (m + 1) / n + р є цілим.
Раціоналізація інтеграла в цих випадках здійснюється наступними підстановками:
1) якщо р - ціле число, то підстановка х = t k. де k - найменше спільне кратне знаменників дробів m і n;
2) якщо (m + 1) / n - ціле число, то підстановка де s -знаменатель дробу р;
3) якщо (m + 1) / n + р - ціле число, то подстановкагде s - знаменник дpобі р.
У всіх інших випадках інтеграли Тіпанов виражаються через відомі елементарні функції, т. е. «не беруть».
Приклад Знайти інтеграл
Рішення: Так як
Тому робимо підстановку