Різноманіття фізичних процесів (змін в часі різних фізичних величин, в тому числі і сигналів електричні-ської зв'язку), з якими можна зустрітися в повсякденному житті, розділяється на два класи.
До першого класу відносяться процеси, протягом яких у часі можна заздалегідь передбачити, маючи деякі апріорні [2] відомості. Наприклад, такі процеси могли б виникнути тільки в повністю ізольованих фізичних системах, де не враховується вплив навколишнього середовища. Такі процеси називаються детермінованими.
Другий клас складають процеси, протягом яких не може бути описано регулярною функцією часу. У кожен даний момент процес з певною ймовірністю може прийняти те чи інше кількісне значення з безлічі можливих. Розглянемо приклад. Відомо, що навіть при постійній різниці потенціалів на електродах радіоламп відзначається хаотичне коливання анодного струму, викликаного флуктуацией інтенсивності потоку електронів, поточних від катода до анода. Явище це називається дробовим ефектом, а викликана ним флуктуація анодного струму - це типовий приклад випадкового процесу. У цьому випадку заздалегідь неможливо описати хід процесу детермінованою функцією часу. Можна тільки вказати для кожного моменту часу розподіл ймовірностей значень процесу.
Випадковий процес X (t) - це особливий вид функція, що характеризується тим, що в будь-який момент часу t прийняті нею значення є випадковими величинами.
Конкретний хід випадкового процесу, встановлений в результаті будь-якого окремого досвіду, називається його реалізацією.
Розмірність окремих реалізацій визначає і розмірність випадкового процесу в цілому. *
Уявити випадковий процес однієї кривою-можливо, але іноді користуються графіком, на якому нанесено декілька реалізації процесу з числа можливих (рис. 1).
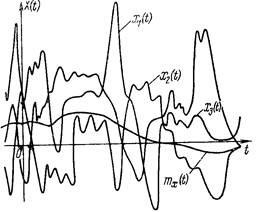
Мал. 1. Сукупність реалізацій безперервного випадкового процесу X (t) і його математичного очікування mx (t)
момент часу t0, то значення випадкового
процесу в цей момент є випадковою величину, звану перетином процесу в точці t0.
Фіксуючи на певному проміжку часу миттєві значення випадкового сигналу, одержуємо лише єдину реалізацію випадкового процесу. Випадковий процес являє собою нескінченну сукупність таких реалізацій, що утворюють статистичний ансамбль. Наприклад, ансамблем є набір сигналів x1 (t), х2 (t).>, Які можна одночасно спостерігати на виходах абсолютно однакових генераторів шумової напруги.
Зовсім необов'язково, щоб реалізації випадкового процесу представлялися функціями зі складним, нерегулярним в часі поведінкою. Часто доводиться розглядати випадкові процеси, утворені, наприклад, всілякими гармонійними сигналами U cos (wt + j), у яких один з трьох параметрів U, w, j - випадкова величина, яка приймає певне значення в кожній реалізації. Випадковий характер такого сигналу укладений в неможливості заздалегідь, до досвіду знати значення цього параметра.
Випадкові процеси, утворені реалізаціями, залежними від кінцевого числа параметрів, прийнято називати квазідетермінірованнимі випадковими процесами.
Різні зв'язкові сигнали, будучи носіями інформації різних повідомлень, є реалізації випадкового процесу.
Випадковим процесом є і перешкода (шум) в каналі зв'язку. Отже, для подальшого вивчення сигналів, перешкод і їх взаємодії при передачі повідомлень, а також для досліджень самого процесу передачі і об'єктивної оцінки різних систем зв'язку необхідно скористатися методами теорії випадкових процесів.
Кількісно випадковий процес описується випадковою функцією часу X (t), яка в будь-який момент часу може набувати різних значень з заданим розподілом ймовірностей.
Залежно від того, які значення приймають аргумент (час t) і рівні реалізації випадкового процесу X, розрізняють чотири типи випадкових процесів.
Безперервний випадковий процес: t і Х можуть приймати будь-які значення на відрізку (або, можливо, на всій) дійсної осі.
Дискретний випадковий процес: t безперервно, а величини Х дискретні (приймають одне з можливих значень з кроком D х).
Безперервна випадкова послідовність: t дискретно (з кроком Dt), а Х може приймати будь-які значення на відрізку (або на всій) числової осі. Такі процеси часто називають також процесами з дискретним часом.
Дискретна випадкова послідовність [3]: t і Х дискретні.
Приклади реалізації чотирьох класів наведені на рис. 2.
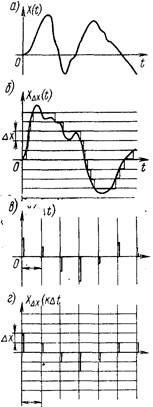
Щоб задати випадковий процес необхідно знати його функцію і щільність розподілу ймовірностей.