У техніці зв'язку для передачі повідомлень використовують безперервні і дискретні сигнали. Якщо джерело виробляє безперервне повідомлення (відповідно параметр сигналу - безперервна функція від часу), відповідна інформація називаетсянепреривной. Прикладом неодмінно-ривного повідомлення служить людська мова, що передається модульованої звуковою хвилею; параметром сигналу в цьому випадку є тиск, що створюється цією хвилею в точці знаходження приймача - людського вуха.
У разі, коли параметр сигналу приймає послідовне в часі кінцеве число значень (при цьому всі вони можуть бути пронумеровані), сигнал називається дискретним. а повідомлення, передане за допомогою таких сигналів - дискретним повідомленням. Інформація, передана джерелом у цьому випадку, також називається дискретною. Приклад дискретного повідомлення - процес читання книги, інформація в якій представлена текстом, тобто дискретної послідовністю окремих символів (букв).
Безперервне повідомлення може бути представлено безперервною функцією, за-даної на деякому відрізку [а, b] (малюнок 2). Але комп'ютер - цифрова машина, тобто внутрішнє подання інформації в ньому дискретно. І для того, щоб за допомогою комп'ютера можна було обробляти безперервне повідомлення. воно повинно бути перетворено в дискретне повідомлення. Така операція можлива. Дискретизація вхідної інформації (якщо вона неперервна) дозволяє зробити її придатною для комп'ютерної обробки.
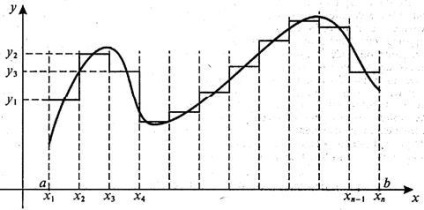
Малюнок 2 - Дискретизація безперервного повідомлення
Дискретизація безперервного повідомлення здійснюється наступним чином. З нескінченної кількості значень неперервної функції (параметра сигналу) вибирається їх певне число, яке наближено може характеризувати інші значення. Один із способів такого вибору полягає в наступному. Область визначення функції розбивається точками x1. x2. хn на відрізки рівної довжини. Ці відрізки (D х) називають інтервалом (кроком) дискретизації. Якщо в якості носія інформації вибрано електричне коливання, то відповідно до теореми Котельникова безперервне повідомлення може бути відновлено з дискретного, якщо інтервал дискретизації вибраний з умови
де Dt - інтервал часу, через який здійснюються вибірки значень неперервної функції (сигналу);
Fмакс - максимальна частота в спектрі сигналу.
На кожному з відрізків D х значення функції приймається постійним і рівним, наприклад, середнього значення на цьому відрізку; отримана на цьому етапі функція називається в математиці ступінчастою. Даний етап називається квантуванням вибірок безперервного повідомлення за рівнем. Наступний крок - проеці-вання значень «сходинок» на вісь значень функції (вісь ординат). Отримана таким чином послідовність значенні функції у1. у2, ..., yn є дискретним поданням неперервної функції, точність якого можна необмежено піднімати шляхом зменшення довжин відрізків розбиття області значень аргументу (D х ® 0).
Ось значень функції можна розбити на відрізки з заданим кроком і що відображається зить кожен з виділених відрізків у відповід-вующий відрізок з безлічі значень. В результаті отримаємо кінцеве безліч чисел, що визначаються, наприклад, по середині або однієї з меж таких відрізків.
Таким чином, перетворення безперервного повідомлення в дискретне здійснюється в два етапи: дискретизація за часом і квантування за рівнем .Любий повідомлення може бути представлено як дискретне, тобто послідовністю знаків деякого алфавіту (наприклад, послідовністю двійкових чисел).