МІНІСТЕРСТВО АГЕНТСТО ОСВІТИ РФ
Рязанська державного радіотехнічного університету
«Синтез частотних характеристик лінійних систем автоматичного регулювання»
Виконав ст. гр. 511
логарифмічна частотна разомкнутая система
1.Построіть логарифмічні частотні характеристики розімкнутої системи за заданими показниками якості.
2. Визначити по побудованим Лах і ЛФХ запаси стійкості по посиленню і по фазі.
3.Запісать передавальну функцію розімкнутої системи по побудованої Лах.
4.Рассчітать і побудувати АЧХ замкнутої системи.
1.Постоянное помилка: по укоріненим (# 948; ст / х0) х 10 2 = 0,5
2.Частота зрізу: # 969; ср (2 + n) · 10 -2 = 3, де n = 1
3.Логаріфміческій коефіцієнт передачі L01 на частоті 0.1 # 969; ср не менше 26дБ.
4.Запас стійкості по фазі # 916; # 966; ± 10 0 = 40 0
5.Постоянние часу обов'язкових інерційних ланок: Тін1 х 10 4 = 7, Тін2 х 10 +5 = 3
6.Частота гармонійної перешкоди (# 969; п / # 969; ср) · 10 -2 = 3
7.Коеффіціент придушення перешкоди Lп не менше 80дБ
Побудова Лах і ЛФХ розімкнутої системи
Побудова Лах починається з низькочастотної асимптоти. Оскільки задана статична помилка то система буде статичною. нахил ЛАХ для низькочастотної асимптоти буде нульовим і помилка визначається виразом # 948; ст = х0 / (1 + k).
k = х0 / # 948; ст -1 = 2 * 10 2 -1 = 199 - коефіцієнт передачі розімкнутої системи
L1 = 20lg (k) = 20lg (199) = 46 - логарифмічний коефіцієнт передачі розімкнутої системи
Тобто низькочастотна асимптота проводиться через т. (1; 46) паралельно осі частот.
Для забезпечення необхідного запасу стійкості по фазі потрібно, щоб Лах перетинала вісь частот під нахилом -20дБ / дек на частоті зрізу.
Побудовані ділянки Лах з'єднуються прямою лінією під нахилом -40дБ / дек, при цьому для забезпечення п.3 вихідних даних вибираємо # 969; з1 = 5рад / с, тоді т. (10; 26) (т. (0.1 # 969; ср; L01)) пройде нижче прямої з нульовим нахилом.
сопрягающую частоту # 969; с2 вибираємо з умови запасу стійкості по фазі # 916; # 966; ± 10 0 = 40 0 (тому що наступні типові і обов'язкові інерційні ланки будуть вносити додатковий фазовий зсув): # 969; с2 = # 969; ср / 2 = 50 рад / с.
Побудована Лах сформована послідовним з'єднанням наступних типових ланок: безінерційним k (p) = 199, двома інерційними k (p) = 1 / (1 + Т1 р) 2 і форсують k (p) = (1 + Т2 p). Т.ч. передавальна функція з'єднання типових ланок матиме вигляд:
ЛФХ отриманої передавальної функції будується складанням ЛФХ окремих ланок.
З рис видно, що при з'єднанні таких типових лінійних ланок, ЛФХ системи не потрапляє в заданий інтервал стійкості по фазі. Для забезпечення цієї умови в систему вводиться додаткове інерційну ланку з сопрягающей частотою # 969; с3 лежить вище частоти зрізу. Система з додатковим інерційним ланкою буде проходити всередині заданого інтервалу при # 969; с3 = 333рад / с.
Добудовуємо Лах і ЛФХ системи з урахуванням введеного ланки, обов'язкових інерційних ланок, п.5 вихідних даних, і перевіряємо вимога до придушення гармонійної перешкоди п.6 і п.7 вихідних даних:
На рис видно, що т. (30 · 10 3; -80) лежить вище Лах розімкнутої системи, отже, вимога до придушення гармонійної перешкоди виконується.
Визначення запасів стійкості
Проведемо графічно по побудованим Лах і ЛФХ розімкнутої системи.
Запас стійкості по посиленню # 916; L = 24дБ.
Запас стійкості по фазі # 916; # 966; = 45 0.
Запис передавальної функції розімкнутої системи по асимптотической Лах
При частотах близьких до 0 Лах має нульовий нахили, значить, формується безінерційним ланкою з передавальної функцією k (p) = k. на # 969; з1 нахил змінюється на - 40 дб / дек - цей нахил забезпечується 2 інерційними ланками з k (p) = 1 / (1 + Т1 р) 2. Т1 = 1 / # 969; з1. З таким нахилом Лах йде до # 969; с2. а потім нахил стає рівним - 20 дб / дек. Зміна нахилу на + 20 дб / дек забезпечується форсують ланкою з k (p) = (1 + Т2 р), Т2 = 1 / # 969; с2. на # 969; с3 нахил змінюється на - 20 дб / дек і стає рівним - 40 дб / дек, т. Е. Діє інерційний ланка з k (p) = 1 / (1 + Т3 р). на # 969; ін1 нахил змінюється на - 20 дб / дек і стає рівним - 60 дб / дек, т. Е. Діє інерційний ланка з k (p) = 1 / (1 + Тін1 р). на # 969; ін2 нахил змінюється на - 20 дб / дек і стає рівним - 80 дб / дек, т. Е. Діє інерційний ланка з k (p) = 1 / (1 + Тін2 р).
При побудові Лах розімкнутої системи використовувалися типові лінійні ланки, тому передавальна функція цієї системи може бути записана як сукупність таких ланок.
,
Генерування незалежних випадкових процесів
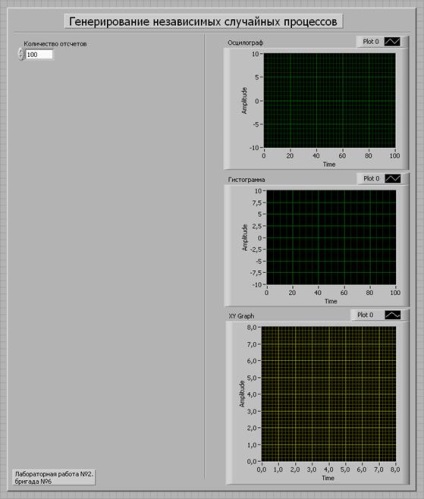
1.Сформіруем лицьову панель відповідно до методичним зазначенням до лабораторної роботи.
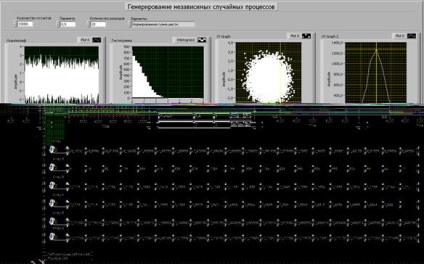
Далі у вікні BlockDiagram додамо відсутні елементи: структуру ForLoop і створимо елемент гістограми. Після чого з'єднаємо всі елементи належним чином. Встановимо кількість відліків рівним 100 і запустимо моделювання.
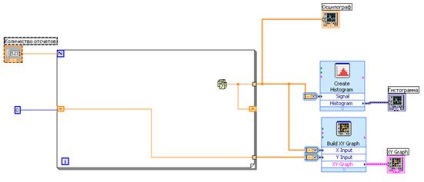
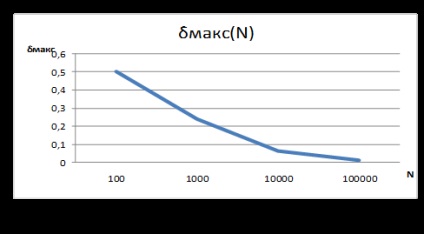
Зробимо обчислення максимальної відносної помилки обчислення ймовірності для різної кількості відліків N:
dмакс = | 10 -15 | / 10 = 0.5
dмакс = | 100 -124 | / 100 = 0.24
dмакс = | 1000 -945 | / 1000 = 0.065
dмакс = | 10000 -10129 | / 10000 = 0.0129
Вважається, що N (кількість експериментів) і m (кількість розрядів) повинні знаходити в наступному співвідношенні:
Такий взаємозв'язок пояснюється тим, що при збільшенні кількості розрядів необхідно збільшувати кількість відліків. Інакше гістограма розподілу буде порізаною і не дозволить судити про розподіл випадкової величини з хорошою точністю.
2.Генерірованіе випадкової послідовності з законом розподілу, відмінним від рівномірного, методом зворотної функції.
Скопіювали структуру ForLoop - генератор рівномірно розподіленої випадкової послідовності. У перемикачі варіантів встановили "Нелінійне перетворення". У утворилося пусте поле вставили скопійоване структуру ForLoop. Всередині структури ForLoopcобралі блок-схему програми по формулі u = s (-2ln (1 - x)) 1/2.
Встановили значення параметра відповідно до варіанта - 0.5 і кількість відліків - 1000.
Запустили моделювання. Складемо таблицю залежності ni (x), pi (x) ,:
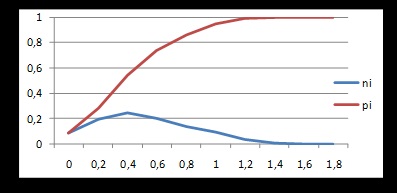
3.Генерірованіе випадкових послідовностей складанням рівномірно розподілених випадкових послідовностей (кількість складаються випадкових величин - від 2 до 6).
Додамо ще 6 варіантів: "Сума двох рівномірних", "Сума трьох рівномірних", "Сума чотирьох рівномірних", "Сума п'яти рівномірних", "Сума шести рівномірних", "Нормована сума шести рівномірних".
Для кожного варіанта зберемо відповідні схеми в структурі Case.
1) Сума двох рівномірних:
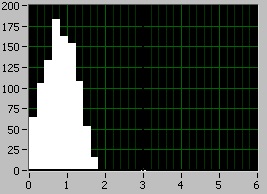
2) Сума трьох рівномірних
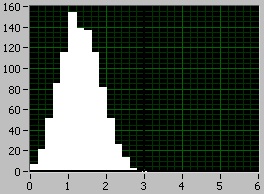
3) Сума чотирьох рівномірних
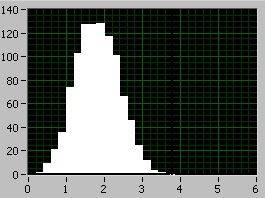
Отримані результати пояснюються тим, що відбувається складання перших і других моментів випадкових величин. Тобто при збільшенні суми на один доданок мат очікування збільшується на 0.5 (значення мат. очікування для рівномірної випадкової величини діапазону 0-1) і десперсія так само збільшується на 1 (значення дисперсії для рівномірної випадкової величини діапазону 0-1).
4.Визначення близькості закону розподілу нормованої суми шести рівномірно розподілених випадкових величин до нормального закону.
У вікнах BlockDiagram і FrontPanel додамо нові елементи, необхідні для вирішення поставленого завдання: