Вираз електричних величин в відносних одиницях широко застосовується в теорії електричних машин. Це обумовлено тим, що подання будь-якої величини не в іменованих, а відносних одиницях істотно спрощує теоретичні викладки і надає результатами розрахунку велику наочність. Переваги системи відносних одиниць:
1) не потрібно стежити за позначеннями;
2) дозволяє вибрати зручні для розрахунку числа;
3) основа теорії подібності дозволяє зв'язати задачі поля з завданнями розрахунку ланцюгів:
Під відносним значенням будь-якої величини слід розуміти її ставлення до іншої однойменної величини, прийнятої за базову:
Отже, перед тим як представити будь-які величини в відносних одиницях, треба вибрати базисні одиниці.
За базисний струм і базисне лінійна напруга приймаються довільні величини Іб. Uб. Тоді базисна потужність трифазного ланцюга буде визначатися формулою:
а базисне опір:
Звідси випливає, що тільки дві базисні величини можуть бути обрані довільно, а інші є пов'язаними. Зазвичай вибирається і Uб. Причому вибрані базисні величини повинні бути єдиними для всієї розрахункової схеми і застосовуватися як до повних величин, так і до їх окремими складовими. Отже, параметри електричної системи в відносних
одиницях при обраних базисних умовах будуть обчислюватися за формулами:
Тут U, I, S, Z - параметри в іменованих одиницях. При розрахунках струмів КЗ прийняті розмірності розрахункових параметрів кВ. кА. МВ · А. М Вт, Мвар, Ом. При цьому всі формули не вимагають додаткових узгоджувальних коефіцієнтів.
При завданні паспортних даних обладнання в відносних одиницях їх параметри відносять до номінальних параметрів елементів:
Так, відносне опір при номінальних умовах показує відносне падіння напруги на елементі при протіканні номінального струму, що надає фізичну наочність параметру:
При розрахунках в системі відносних одиниць вихідні параметри зазвичай задаються або в іменованих одиницях (і.є.) або в відносних одиницях (в.о.) при номінальних умовах елемента. При побудові розрахункових схем заміщення потрібно їх переклад в відносні одиниці при базисних умовах з обов'язковим приведенням параметрів на основну щабель.
При цьому для побудови розрахункових формул потрібно рішення двох завдань:
1) задані параметри в і.є. - потрібно їх переклад у в.о. при базисних умовах з приведенням на основну щабель;
2) задані параметри в в.о. при номінальних умовах - потрібно їх переклад у в.о. при базисних умовах з приведенням на основну щабель.
Розглянемо порядок побудови розрахункових формул на прикладі опорів і ЕРС.
Тут: - базисне напруга, наведене на розрахункову ступінь.
Формули (4.17) і (4.18) є формулами точного приведення. При наближеному приведення
де - номінальна напруга ступені, де встановлений елемент.
При звично використовуються умови формули приймають вид:
Тут - номінальне паспортне напругу елемента.
Формули (4.22) і (4.23) є формулами точного приведення. При наближеному приведення
При зазвичай використовуваних умовах і формули набувають вигляду:
Надалі індекс приведення буде опускатися.
4.4. Визначення опору елементів електричних систем
і їх схеми заміщення
Формули визначення опорів наведені в відносних одиницях при наближеному приведення до базисних умов.
Генератори. У генераторів практично ніколи не враховується активний опір, так як воно зневажливо мало в порівнянні з індуктивним. Номінальний опір генератора в відносних одиницях може бути визначено з паспортних даних:
-, - синхронні опору по поздовжньої і поперечної осі, які характеризують сталий режим.
- і, і - перехідні і сверхпереходние опору в момент часу t = 0.
-, - опору зворотної та нульової послідовностей.
Номінальний опір генератора у відносних одиницях при базисних умовах визначається формулою:.
Двигуни. Параметри синхронних електродвигунів визначаються ана ло гі-ч-но генераторам.
Реактори. Струмообмежувальним реактори можуть мати різне пристрій і конструктивне виконання, а також технічні та техніко-економічні характеристики і параметри.
Лінійні реактори. включаються послідовно в відповідну лінію, обмежують струм КЗ і підтримують відносно високий рівень залишкового напруги. Опір лінійного реактора можна визначити за формулою:
, де лежить в межах 0,1 ... 0,4 Ом.
Здвоєний реактор має кращі характеристики. Між гілками реактора існує магнітна зв'язок, яка в наскрізному режимі дозволяє зменшити втрати напруги в реакторі. Коефіцієнт магнітної зв'язку ідентичних гілок обмотки реактора дорівнює:
Здвоєний реактор має 3 режими роботи (рис. 4.11)
Одинланцюговому режим (рис. 4.11а). У одинланцюговому режимі загальний опір реактора визначаться як опір однієї його гілки:
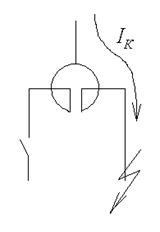
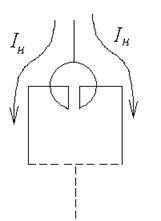
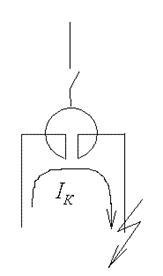
Мал. 4.11. Режими роботи здвоєного реактора
Дволанцюгова (наскрізний) режим (рис. 4.11б). Дволанцюгова режим - це нормальний режим роботи реактора. У такому режимі магнітні потоківетвейнаправлени зустрічно, що викликає зменшення індуктивного опору однієї гілки.
Індуктивний опір однієї гілки:.
Загальна індуктивний опір:.
Поздовжній режим (рис. 4.11в). У поздовжньому режимі магнітні потоки ветвейнаправлени згідно і індуктивність гілки збільшується.
Кожен режим роботи реактора може бути представлений своєю схемою заміщення. Активний опір зазвичай не враховується, але воно може бути знайдено за втратами активної потужності в реакторі. На малюнку 3 наведена загальна схема заміщення здвоєного реактора.
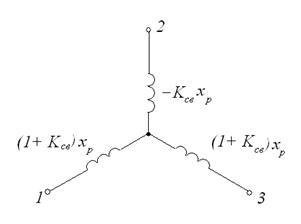
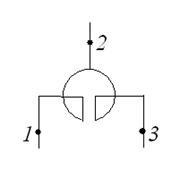
Мал. 4.12. Позначення здвоєного реактора і його схема заміщення
Розглянемо приклад. Використовуючи схему заміщення (рис. 4.12), визначимо опір реактора в одинланцюговому, наскрізному і поздовжньому режимах. Коефіцієнт зв'язку дорівнює 0,5.
У режимі КЗ (одинланцюговому):
У нормальному (наскрізному) режимі:
У поздовжньому режимі:
Активний опір трансформатора:
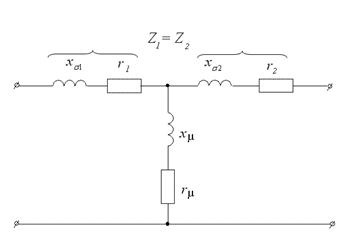
Нехтуючи гілкою намагнічування, отримаємо спрощену схему заміщення (рис. 4.16):
Мал. 4.16. схема заміщення
Активний опір трансформатора в відносних одиницях, наведене до базисних умов:
де - номінальне активний опір у відносних одиницях.
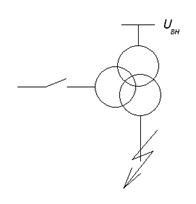
Мал. 4.17. Умовне позначення і схема заміщення трёхобмоточного трансформатора
У відносних одиницях напруги короткого замикання обмоток будуть дорівнювати їх опорам розсіювання і їх значення для обмоток вищої, середньої та нижчої напруг триобмоткового трансформатора можуть бути визначені за формулами:
Дані формули справедливі і для автотрансформатора, зазвичай в розрахунки не вводиться.
Трансформатор з розщепленої обмоткою. На електростанціях і підстанціях застосовуються силові трансформатори і автотрансформатори з розщепленої обмоткою нижчої напруги, так як це дозволяє істотно знизити струм КЗ в мережах низької напруги. Підвищувальні трансформатори і автотрансформатори з розщепленої обмоткою використовуються для формування укрупнених блоків електростанцій, особливо на ГЕС.
Мал. 4.18 Умовне позначення трансформатора з розщепленої обмоткою:
а) обмотка нижчої напруги розщеплена на 2 частини;
б) обмотки нижчої напруги розщеплена на 3 частини
Опір трансформатора з розщепленої обмоткою характеризується наступними параметрами:
- опір розщеплення, рівний опору між висновками двох довільних частин розщепленої обмотки;
- наскрізне опір, рівний опору між висновками обмотки вищого напруги і об'єднаними висновками частин розщепленої обмотки нижчої напруги;
- коефіцієнт розщеплення, рівний відношенню опору розщеплення до наскрізного опору:
При розщепленні обмотки на дві частини (рис. 4.18а), а при розщепленні на три частини (рис. 4.18б). Коефіцієнт розщеплення також залежить від виконання трансформатора, наприклад, для трансформатора броньового виконання (рис. 4.18а) при відсутності інших даних слід приймати. Для групи однофазних трансформаторів.
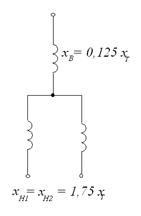
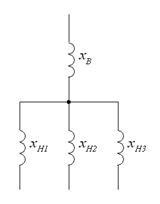
Мал. 4.19 Схеми заміщення трансформатора з розщепленої обмоткою
Опір розсіювання обмоток трансформатора:
При розщепленні нижчої обмотки на 2 частини (рис. 4.19а) опір обмоток нижчої напруги:
Опір обмотки вищого напруги:
Для трансформатора стрижневі типу і схеми заміщення для активних і індуктивних опорів наведені на рис. 4.19б, в.
При розщепленні нижчої обмотки на 3 частини (рис. 4.19г) опір обмотки вищого напруги:.
Опір обмоток нижчої напруги:
Приклад. Автотрансформатор з розщепленої обмоткою нижчої напруги на 2 частини (рис. 4.20).
Опір розщеплених обмоток нижчої напруги:
Опору обмоток вищої, середньої та нижчої напруг:
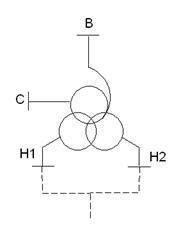
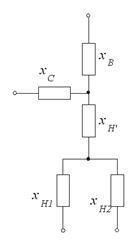
Мал. 4.20. Автотрансформатор з розщепленої обмоткою і його схема заміщення