Розкладання вектора по ортам координатних осей.
Модуль вектора. направляючі косинуси
Розглянемо в просторі прямокутну систему координат Охуг. Виділимо на координатних осях Ох, Оy і Оz одиничні вектори (орти), що позначаються. . відповідно (рис. 2.5).
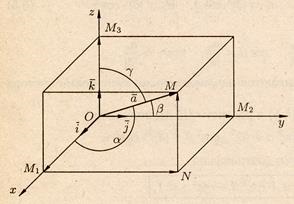
Виберемо довільний вектор простору і сумісний його початок з початком координат:.
Проведемо через ко-нец вектора площини, парал-лельно координатним площинам. Точки перетину цих площин з осями позначимо відповідно че-рез. . . Отримаємо прямо-вугільний паралелепіпед, однією з діагоналей якого є вектор.
Тоді, використовуючи визначення суми векторів, послідовно отримуємо.
Координати вектора в базисі. . позначимо x. у, z. Таким чином, координати точки М (x. У, z) - це також і координати. Поет-му = х + y + z.
Спрямовані прямі, що проходять через точку О і сонаправленнимі з базисними векторами. . називаються осями координат відпо-відно Ох, Оy і Оz. Координати вектора (x. У, z) - це проекції вектора на осі Ох, Оy і Оz.
Знайти вектор. якщо А (5; 8; -1), В (1; 3; 2).
Для випадку площині декартова система координат визначаються-ється початком координат Про і двома базисними векторами. .
Відповідно застосовуються записи для точки площині М (х, у) і вектора в площині (x, у).
Знайти орт вектора.
З рішення отримуємо.
Вектори і колінеарні (паралельні). З рівності векторів і треба рівність відповідних координат bx = lax. by = lay. bz = laz. З цих трьох рівностей виходить умова коллинеарности векторів і: