Задати рух точки означає поставити її положення в кожен момент часу. Положення це має визначатися, як уже зазначалося, в будь-якій системі координат. Однак для цього не обов'язково завжди задавати самі координати; можна використовувати величини, так чи інакше з ними пов'язані. Нижче описані три основні способи завдання руху точки.
1. Природний спосіб. Цим способом користуються, якщо відома траєкторія руху точки. Траєкторією називається сукупність точок простору, через які проходить рухається матеріальна частинка. Це лінія, яку вона викреслює в просторі. За природного способу необхідно задати (рис. 1):
а) траєкторію руху (щодо будь-якої системи координат);
б) довільну точку на ній нуль, від якого відраховують відстань S до рухається частинки уздовж траєкторії;
в) позитивний напрямок відліку S (при зміщенні точки М в протилежному напрямку S негативно);
г) початок відліку часу t;
д) функцію S (t), яка називається законом руху **) точки.
2. Координатний спосіб. Це найбільш універсальний і вичерпний спосіб опису руху. Він передбачає завдання:
а) системи координат (не обов'язково декартовой) q1, q2, q3;
б) початок відліку часу t;
в) закони руху точки, тобто функцій q1 (t), q2 (t), q3 (t).
Говорячи про координати точки, ми завжди будемо мати на увазі (якщо не визначено інше) її декартові координати.
3. Векторний спосіб. Положення точки в просторі може бути визначено також і радіус-вектором, проведеним з деякого початку в дану точку (рис. 2). В цьому випадку для опису руху необхідно задати:
а) початок відліку радіус-вектора r;
б) початок відліку часу t;
в) закон руху точки r (t).
Прискорення точки. [М / с 2]. Проекції уск.-я: і т.д. Модуль уск.-я. направляюча. косинуси. і т.д.
При завданні руху в полярних координатах: проекції прискорення на радіальний напрямок. поперечний напрям. модуль прискорення. При природним сп. завдання руху повне прискорення розкладають на нормальне і дотичне (тангенціальне) прискорення. Модуль нормального прискорення. r - радіус кривизни траєкторії, нормальне прискорення направлено по нормалі до траєкторії (^ до дотичній) завжди до центру кривизни, тобто в сторону угнутості. Нормальне прискорення характеризує зміну швидкості за напрямком. Модуль дотичного прискорення. направлено по дотичній до траєкторії, або в сторону швидкості, або у зворотний. Дотичне прискорення характеризує зміну швидкості за величиною. При прискореному руху-ії напрямок касатся. УСК. і швидкості збігаються, при уповільненому - протилежно. ^. Þ. Вектор прискорення лежить в дотичній площині Þ його проекція на бінормаль дорівнює 0 (головна нормаль лежить в дотичній площині, тобто в площині плоскої кривої, бінормаль - ^ до головної нормалі і дотичній). Окремі випадки руху точки:
1) Прямолінійний: радіус кривизни r = ¥ (нескінченно великий) Þ аn = 0, a = at.
2) Рівномірний криволінійне рух-ие: v = const Þ at = 0, a = an. Уск. з'являється тільки за рахунок зміни напрямку швидкості. Закон движ-ия: s = s0 + v × t, при s0 = 0 v = s / t.
3) Рівномірний прямолінійний рух-ие: а = at = an = 0. Єдине движ-ие, де а = 0.
4) равнопеременное криволінійне рух-ие: at = const, v = v0 + at × t. При равноуск. русі знаки у at і v однакові, при равнозамедленно - різні.
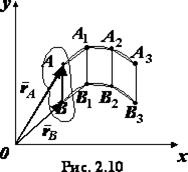
Теорема. При поступальному русі твердого тіла всі його точки рухаються по однаковим і паралельних траєкторіями і мають в кожен даний момент часу рівні по модулю і напрямку швидкості і прискорення.
Доведення. Для доведення теореми розглянемо рух відрізка прямої. проведеного в тілі, що здійснює поступальний рух (рис. 2.10). З визначення поступального руху слід, що в кожен даний момент часу відрізок. займає послідовно положення. . і т.д. залишається паралельним свого початкового стану. З огляду на це і те що. робимо висновок, що ламані лінії і паралельні і при накладенні співпадуть усіма своїми точками. При нескінченному зменшенні проміжків часу між розглянутими положеннями відрізка ми бачимо, що точка і точка описують однакові криві, т. Е. Криві, що збігаються при накладанні.
Для доказу другої частини теореми зауважимо, що
Візьмемо похідні за часом від лівої і правої частин
Розібрана теорема дозволяє зробити висновок, що поступальний рух твердого тіла цілком визначається рухом якої-небудь однієї його точки