Властивості додавання, віднімання, множення і ділення корисні тим, що дозволяють перетворювати суми і твори в зручні вираження для обчислень. Навчимося, як можна за допомогою цих властивостей спрощувати вирази.
52 + 287 + 48 + 13 =
У цьому виразі є числа, при додаванні яких виходять «круглі» числа. Помітивши це, легко провести обчислення усно. Скористаємося переместітельним законом складання.
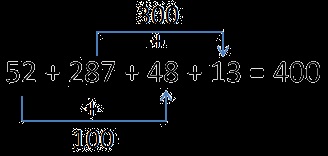
Також для спрощення обчислення творів можна використовувати переместітельний закон множення.
7 · 2 · 9 · 5 = (2 · 5) · (7 · 9) = 10 · 63 = 630
Сочетательних і переместітельності властивості використовуються і при спрощення буквених виразів.
- 6 · a · 2 = 6 · 2 · a = 12a
- 2 · a · 4 · b = 2 · 4 · a · b = 8ab
- 5b + 8b = (5 + 8) · b = 13b
- 14y - 12y = (14 - 12) · y = 2y
Розподільчий закон множення часто застосовується для спрощення обчислень.
Застосовуючи розподільна властивість множення відносно додавання або віднімання до вираження «(a + b) · с і (a - b) · c», ми отримуємо вираз, що не містить дужки.
У цьому випадку говорять, що ми розкрили (опустили) дужки. Для застосування властивостей не має значення, де записаний множник «c» - перед дужками або після.
Розкриємо дужки у виразах.
- 2 (t + 8) = 2t + 16
- (3x - 5) 4 = 4 · 3x - 4 · 5 = 12x - 20
Якщо перед літери не записано число, то мається на увазі, що перед буквою стоїть числовий множник 1.
Винесення спільного множника за дужки
Поміняємо місцями праву і ліву частину рівності:
У таких випадках кажуть, що з «ac + bc» винесено загальний множник «с» за дужки.
Приклади винесення загального множника за дужки.
- 73 · 8 + 7 · 8 = (73 + 7) · 8 = 80 · 8 = 640
- 7x - x - 6 = (7 - 1) x - 6 = 6x - 6 = 6 (x - 1)