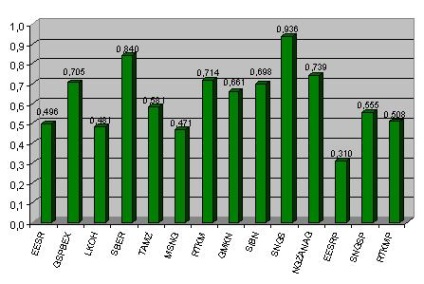
Мал. 3.5 - коефіцієнт бета акцій
Для складання оптимального портфеля досить визначення математичного очікування як арифметичної середньої минулих доходностей (рисунок 3.6). Математичне сподівання не відображає дійсний прогноз прибутковості акцій, який проводиться на основі всіх факторів, що впливають, але воно досить для застосування математичних моделей побудови оптимального портфеля цінних паперів.
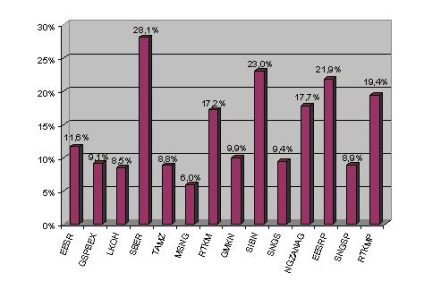
Мал. 3.6. Математичне сподівання прибутковості акцій
Знайдемо тепер структуру оптимального портфеля акцій. Для проведення розрахунків необхідно задати безрисковую прибутковість. За безризикову ставку приймемо очікувану прибутковість портфеля ОФЗ, розраховану раніше і рівну 6% річних. Хоча в розрахованому портфелі державних облігацій присутня деяка частка ризику, з деякими припущеннями прибутковість по ньому можна прийняти в якості безризикової.
Очікувана прибутковість портфеля розраховується як зважене середнє математичних очікувань прибутковості входять до нього цінних паперів, де в якості ваг взяті частки інвестицій, що припадають на ці папери (формула 17).
На малюнку 3.7 відображена структура розрахованого портфеля акцій. Портфель складається з непропорційних частин: половина акцій займають 86,6% портфеля, інша половина - всього лише 13,4%. Найбільша частка виділена простим акціям Товариства з обмеженою відповідальністю «Керуюча компанія« Нафтогазові активи »(« Нафтогазові активи ») - 28,8% .Компанія« Ростелеком »представлена в портфелі двома видами акцій (прості - 13,6%, привілейовані - 15, 5%), то найбільша частка даного портфеля належить акціям саме цієї компанії (29,1%).
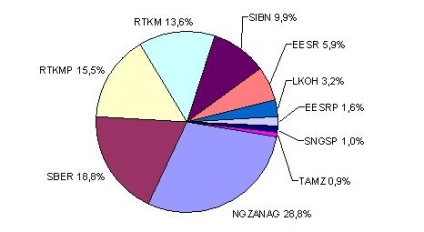
Мал. 3.7. Структура оптимального портфеля акцій
Визначення оптимальних портфелів державних облігацій і акцій не достатньо для складання кінцевого портфеля цінних паперів. Необхідно також вирішити в яких пропорціях будуть інвестуватися кошти в ці портфелі.
Для визначення цих пропорцій скористаємося моделлю Марковіца, застосованої при знаходженні оптимального портфеля облігацій.
Характерною особливістю в даному випадку буде те, що в якості розглянутих одиниць будуть виступати не окремі цінні папери, а самі портфелі цінних паперів. Тому інтерес буде представляти динаміка прибутковості портфелів, а динаміка прибутковості окремих їх складових в розрахунок братися не буде.
При складанні портфеля акцій той факт, що ціни були номіновані в доларах США, не впливав на кінцевий результат у вигляді частки цінних паперів в портфелі. В даному випадку при визначенні ковариаций з портфелем облігацій, вираженому в рублях, можуть виникнути розбіжності. Тому виникає необхідність перерахунку прибутковості акцій, виходячи з котирувань акцій в рублях.
Для вирішення задачі знаходження оптимальної структури сукупного портфеля цінних паперів будемо використовувати модель Марковіца.
Для побудови ефективної безлічі можливих портфелів необхідно обчислити математичне сподівання і ковариационную матрицю.
Прибутковість портфеля облігацій за місяць була знайдена простим діленням річної прибутковості на 12. Недільна прибутковість портфеля акцій була приведена до місячної шляхом множення на кількість тижнів.
Математичне сподівання прибутковості портфеля в даному випадку розраховане не як арифметичне середнє, а за нього прийнята очікувана прибутковість, отримана в попередньому параграфі. Вона є більш точною величиною.
Для складання ковариационной матриці необхідно розрахувати середньоквадратичне відхилення прибутковості портфелів і коефіцієнт кореляції між ними (таблиця 3.8).
Коваріації розраховані на основі формули (18). Результати зведені в таблиці 3.9. Коваріації портфеля облігацій і портфеля акцій рівні середньоквадратичного відхилення, зведеному в квадрат, тобто дисперсії цих портфелів.
Вихідні дані для оптимізації сукупного портфеля
На основі цих даних можливо побудувати ефективну безліч портфелів. Математичне сподівання прибутковості портфеля визначається як середньозважене доходностей, де в якості ваги виступає частка інвестицій до окрему цінний папір (формула 17). Ризик кожного портфеля визначений за формулою (18). Результати розрахунків наведені в додатку 2. На основі цих даних можливо побудувати ефективну безліч можливих сукупних портфелів цінних паперів (рисунок 3.8).
Тепер необхідно визначити місце розташування оптимального портфеля, тобто вибрати прийнятне співвідношення дохідності та ризику.
Так як банки є організаціями, не схильними до великому ризику, то шукана точка повинна знаходитися в лівій частині кривої - з меншим ризиком. Починаючи з певного моменту, крива набуває все більш пологий вигляд, що свідчить про те, що при подальшому збільшенні прибутковості ризик збільшується наростаючими темпами. Тому, доцільно за оптимальний портфель для даного інвестора прийняти портфель з дохідністю 15,2%.
Таким чином, в даному портфелі облігації мають 45%, а акції представлені 55%.
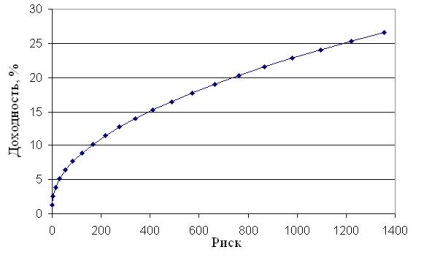
Мал. 3.8. Ефективне безліч сукупних портфелів
До сих пір склад портфеля визначався в відносних величинах. Для подальшої оцінки результатів необхідні абсолютні значення. Тому необхідно визначити кількісний склад портфелів. Для цього необхідно вибрати суму інвестованих коштів.
У період, коли Альфа-банк активно займався операціями купівлі-продажу цінних паперів, сума коштів, що інвестуються доходила до 15% від валюти балансу. Валюта балансу становила близько 340 млн. Рублів. Вважаю за доцільне взяти за розмір інвестування суму в 5 млн. Рублів, що становить приблизно 1,5% валюти балансу і порівнянно з величиною статей звітності.
Таким чином, з огляду на, що 45% коштів інвестується в ОФЗ, а 55% - в акції, отримаємо, що 2250 тис. Руб. має бути направлено на покупку ОФЗ, а частина, що залишилася (2750 тис. руб.) - на покупку акцій.
Кількість облігацій для покупки розраховується за формулою:
де Ki - кількість цінних облігацій, шт .;
di - частка портфеля, яку займає облігацією;
S - сума коштів, що інвестується в портфель, руб .;
P% - ціна облігації, в% від номіналу;
N - номінал облігації, руб.
Дані для розрахунку і результати зведені в таблицю 3.10.
Розрахунок кількості облігацій для покупки
Розрахунок кількості акцій для покупки в портфель
Сума коштів, що інвестуються, руб.
3.3 Управління портфелем цінних паперів Альфа - Банку в сучасних умовах
Розрахунок зміни вартості портфеля ОФЗ