Потік вектора магнітної індукції крізь будь-яку замкнену поверхню дорівнює нулю:
Ця теорема відображає факт відсутності магнітних зарядів, внаслідок чого лінії магнітної індукції не мають ні початку, ні кінця і є замкнутими.
Отже, для потоків векторів В і Е крізь замкнуту поверхню в вихровому і потенційному полях виходять різні вирази.
Як приклад розрахуємо потік вектора В крізь соленоїд. Магнітна індукція однорідного поля всередині соленоїда з сердечником з магнітною проникними-мостью m. згідно (119.2), дорівнює B = # 956; 0 # 956; NI / l
Магнітний потік крізь один виток соленоїда площею S дорівнює Ф1 = BS
а повний магнітний потік, зчеплений з усіма витками соленоїда і званий потокозчеплення,
Аналогічно циркуляції вектора напруженості електростатичного поля вводиться циркуляція вектора магнітної індукції. Циркуляцією вектора В по заданно-му замкнутому контуру називається інтеграл
,
де dl - вектор елементарної довжини контуру, спрямованої уздовж обходу контуру, Bl = B cosa - складова вектора В в напрямку дотичної до контуру (з урахуванням обраного напрямку обходу), a - кут між векторами В і dl.
Закон повного струму для магнітного поля у вакуумі (теорема про циркуляцію вектора В): циркуляція вектора В за довільним замкнутому контуру дорівнює добутку магнітної постійної m0 на алгебраїчну суму струмів, які охоплюються цим кон-туром:
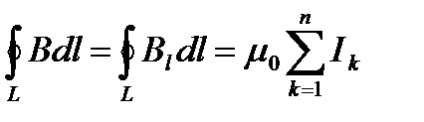
де n - число провідників зі струмами, які охоплюються контуром L довільної форми. Кожен ток враховується стільки разів, скільки разів він охоплюється контуром. Позитивним вважається струм, напрямок якого утворює з напрямком обходу по контуру правовінтовую систему; ток протилежного напрямку вважається негативним.
Порівнюючи вирази для циркуляції векторів Е і В. бачимо, що між ними існує принципова відмінність. Циркуляція вектора Е електростат-чеського поля завжди дорівнює нулю, т. Е. Електростатичне поле є потенціалом-ним. Циркуляція вектора В магнітного поля не дорівнює нулю. Таке поле називається вихровим.
Теорема про циркуляцію вектора В має в навчанні про магнітне поле таке ж значення, як теорема Гаусса в електростатики, так як дозволяє знаходити магнітну індукцію поля без застосування закону Біо - Савара- Лапласа.
Лінії магнітної індукції неперервні: вони не мають ні початку, ні кінця. Це має місце для будь-якого магнітного поля, викликаного якими завгодно контурами зі струмом. Векторні поля, що володіють безперервними лініями, отримали назву вихрових полів. Ми бачимо, що магнітне поле є вихровий поле. У цьому полягає істотна відмінність магнітного поля від електростатичного.
В електростатичному полі лінії напруженості завжди розімкнуті: вони починаються і закінчуються на електричних зарядах. Лінії же індукції магнітного поля не мають ні початку, ні кінця. Це відповідає тому, що в природі немає магнітних зарядів.
Рух електричних зарядів є електричний струм. Так як магнітних зарядів немає, то магнітного струму не існує.