Нехай тіло обмежена площинами і. Нехай кожне перетин тіла площиною є квадрованою фігура. причому її площа є безперервною функцією на відрізку. Тоді тіло буде кубіруемо і його обсяг обчислюється за формулою.
Розглянемо розбиття відрізка кінцевим набором точок
. Тоді. де обсяг частини тіла, укладеної між площинами і. У кожному частковому відрізку розбиття виберемо точку. Перетин тіла площиною є квадрованою фігура. Площа - безперервна функція, отже, якщо відрізок досить малий, то на ньому змінюється мало, значить можна вважати, що. Тоді обсяг приблизно дорівнює обсягу призми з площею підстави і висотою .Враховуючи формулу обсягу призми, отримуємо. Тоді обсяг усього тіла наближено дорівнює. Так як в правій частині цієї рівності стоїть інтегральна сума Рімана для функції на відрізку. то при дрібноту розбиття прагне до нуля, отримуємо формулу.
Приклад. Знайти обсяг еліпсоїда.
Рішення. Запишемо рівняння еліпсоїда:.
Знайдемо перетин еліпсоїда площиною:
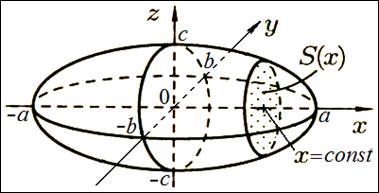
У перетині еліпсоїда площиною вийшов еліпс з півосями
і. Площа цього еліпса дорівнює
. Підставляючи в формулу обчислення об'єму тіла через площу поперечних перерізів, отримуємо
В окремому випадку, коли всі півосі еліпсоїда однакові і рівні. отримуємо формулу обсягу кулі.