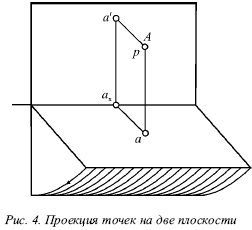
Розглянемо проекції точок на дві площини, для чого візьмемо дві перпендикулярні площині (рис. 4), які будемо називати горизонтальній фронтальної і площинами. Лінію перетину даних площин називають віссю проекцій. На розглянуті площині спроеціруем одну точку А за допомогою плоскої проекції. Для цього необхідно опустити з даної точки перпендикуляри Аа і A на розглянуті площині.
Проекцію на горизонтальну площину називають горизонтальною проекцією точки А. а проекцію а на фронтальну площину називають фронтальною проекцією.
Точки, які підлягають проецированию, в нарисної геометрії прийнято позначати за допомогою великих латинських букв А, В, С. Для позначення горизонтальних проекцій точок застосовують малі літери а, b, с ... Фронтальні проекції позначають малими літерами з штрихом вгорі а, b, с ...
Застосовується також і позначення точок римськими цифрами I, II, ... а для їх проекцій - арабськими цифрами 1, 2 ... і 1, 2 ...
При повороті горизонтальній площині на 90 ° можна отримати креслення, в якому обидві площині знаходяться в одній площині (рис. 5). Дана картина називається епюр точки.
Через перпендикулярні прямі Аа і Аа проведемо площину (рис. 4). Отримана площину є перпендикулярній фронтальній і горизонтальній площинах, тому що містить перпендикуляри до цих площинах. Отже, дана площину перпендикулярна лінії перетину площин. Отримана пряма перетинає горизонтальну площину по прямій аах. а фронтальну площину - по прямій аах. Прямі аах і аах є перпендикулярними осі перетину площин. Тобто Ааах є прямокутником.
При суміщенні горизонтальній і фронтальній площин проекції а й а будуть лежати на одному перпендикуляр до осі перетину площин, так як при обертанні горизонтальній площині перпендикулярність відрізків аах і аах не порушується.
Отримуємо, що на епюрі проекції а й а деякою точки А завжди лежать на одному перпендикуляр до осі перетину площин.
Дві проекції а й а деякою точки А можуть однозначно визначити її положення в просторі (рис. 4). Це підтверджується тим, що при побудові перпендикуляра з проекції а до горизонтальної площини він пройде через точку А. Точно так же перпендикуляр з проекції а до фронтальної площини пройде через точку А. т. Е. Точка А знаходиться одночасно на двох конкретних прямих. Точка А є їхньою точкою перетину, т. Е. Є певною.
Розглянемо прямокутник Aaaха (рис. 5), для якого справедливі наступні твердження:
1) Відстань точки А від фронтальної площини дорівнює відстані її горизонтальної проекції а від осі перетину площин, т. Е.
2) відстань точки А від горизонтальної площини проекцій дорівнює відстані її фронтальної проекції а від осі перетину площин, т. Е.
Інакше кажучи, навіть без самої точки на епюрі, використовуючи тільки дві її проекції, можна дізнатися, на якій відстані від кожної з площин проекцій знаходиться дана точка.
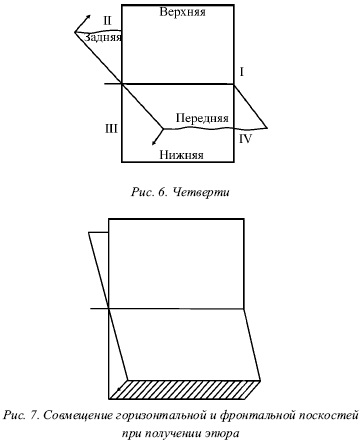
Перетин двох площин проекцій розділяє простір на чотири частини, які називають чвертями (рис. 6).
Ось перетину площин ділить горизонтальну площину на дві чверті - передню і задню, а фронтальну площину - на верхню і нижню чверті. Верхню частину фронтальної площини і передню частину горизонтальній площині розглядають як межі першої чверті.
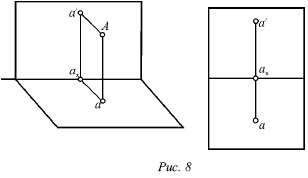
При отриманні епюра обертається горизонтальна площина і поєднується з фронтальним площиною (рис. 7). У цьому випадку передня частина горизонтальній площині співпаде з нижньою частиною фронтальної площини, а задня частина горизонтальній площині - з верхньою частиною фронтальної площини.
На малюнках 8 # 8209; 11 показані точки А, В, С, D, що розташовуються в різних чвертях простору. Точка А розташована в першій чверті, точка В - у другій, точка С - в третій і точка D - в четвертій.
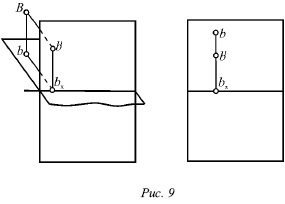
При розташуванні точок в першій або четвертій чвертях їх горизонтальні проекції знаходяться на передній частині горизонтальній площині, а на епюрі вони ляжуть нижче осі перетину площин. Коли точка розташована в другій або третій чверті, її горизонтальна проекція буде лежати на задній частині горизонтальній площині, а на епюрі буде знаходитися вище осі перетину площин.
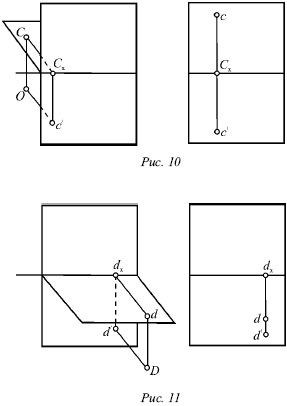
Фронтальні проекції точок, які розташовані в першій або другій чвертях, будуть лежати на верхній частині фронтальній площині, а на епюрі будуть знаходитися вище осі перетину площин. Коли точка розташована в третій або четвертій чверті, її фронтальна проекція - нижче осі перетину площин.
Найчастіше при реальних побудовах фігуру розташовують в першій чверті простору.
У деяких окремих випадках точка (Е) може лежати на горизонтальній площині (рис. 12). У цьому випадку її горизонтальна проекція е і сама точка будуть збігатися. Фронтальна проекція такої точки буде перебувати на осі перетину площин.
У разі, коли точка К лежить на фронтальній площині (рис. 13), її горизонтальна проекція k лежить на осі перетину площин, а фронтальна k показує фактичне місцезнаходження цієї точки.
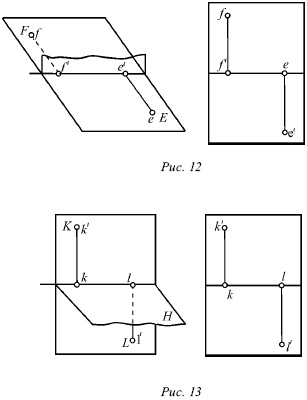
Для подібних точок ознакою того, що вона лежить на одній з площин проекцій, є те, що одна її проекція знаходиться на осі перетину площин.
Якщо точка лежить на осі перетину площин проекцій, вона і обидві її проекції збігаються.
Коли точка не лежить на площинах проекцій, вона називається точкою загального положення. Надалі, якщо немає особливих відміток, розглянута точка є точкою загального положення.