Мета уроку
• Ознайомитись школярів з теоремою Піфагора;
• Сформулювати і довести теорему Піфагора;
• Ознайомити школярів з різними методами застосування цієї теореми при вирішенні завдань;
• Формувати навички використання отриманих знань на практиці;
• Розвивати увагу учнів, самостійність і інтерес до геометрії;
• Виховувати культуру математичної мови.
завдання уроку
• Навчитися використовувати властивості фігур при виконанні завдань.
• Вміти застосовувати теорему Піфагора під час вирішення завдань.
план уроку
• Короткі біографічні відомості.
• Теорема і її доказ.
• Цікаві факти.
• Вирішення задач.
• Домашнє завдання.
Короткі біографічні відомості про Піфагора

На жаль, Піфагор не залишив ніяких творів про свою біографію, тому всі відомості про цю велику філософа і знаменитому математики ми можемо дізнатися тільки завдяки спогадам його послідовників, та й то не завжди справедливих. Тому про цю людину ходить багато легенд. Але правда полягає в тому, що Піфагор був великим еллінським мудрецем, філософом і талановитим математиком.
За недостовірними відомостями, великий мудрець і геніальний вчений Піфагор народився в далеко не бідній сім'ї, на острові Самос, приблизно в 570 році до н.е.
Поява на світ геніального дитини напророкувала Пафія. Тому майбутній світила отримав своє ім'я Піфагор, яке позначає, що це саме той, про кого оголосила Пафія. Вона передбачила, що народжене немовля в майбутньому принесе чимало користі і добра людям.
Новонароджений був шалено красивий, а современем порадував оточуючих своїми видатними здібностями. А так як юне обдарування коротати свої дні серед мудрих старців, то в майбутньому це принесло свої плоди. Ось так завдяки Гермодаманту Піфагор полюбив музику, а Ферекид направив розум дитини до логосу. Після життя в Самос Піфагор отпправілся в Мілеет, де відбулося знайомство ще з одним вченим - Фалесом.
Піфагор познайомився зі знаннями всіх відомих на той час мудреців, так як був допущений до навчання і пізнання всіх таїнств, які були іншим заборонені. Він намагався докопатися до істини і увібрати всі накопичені людством знання.
Після двадцяти двох років перебування в Єгипті, Піфагор перебрався в Вавилон, де продовжив своє спілкування з різними мудрецями і магами. Повернувшись в кінці свого життя в Саміос, він був визнаний одним з наймудріших людей того часу.
теорема Піфагора
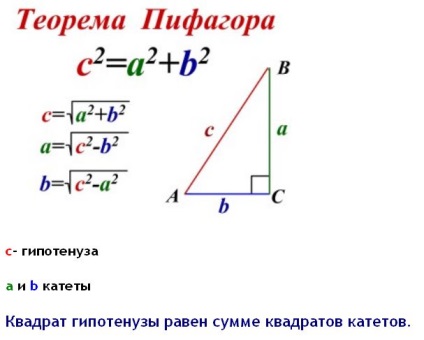
Навіть людина, якій поки не довелось вивчати цю теорему, напевно чув висловлювання про «піфагорових штанях». Особливість цієї теореми в тому, що вона стала однією з ключових теорем евклідової геометрії. Вона дозволяє легко знайти і встановити відповідність між сторонами прямокутного трикутника.
Теорема Піфагора запам'яталася кожному школяреві не тільки висловлюванням: «піфагорові штани на всі сторони рівні», а своєю простотою і значущістю. І на перший погляд ця теорема хоча і здається простою, але має велике значення, так як в геометрії вона застосовується практично на кожному кроці.
Теорема Піфагора налічує велику кількість різних доказів і, напевно, є єдиною теоремою, яка має таке величезне число доказів. Така різноманітність підкреслює безмежну значимість цієї теореми
У теоремі Піфагора присутні геометричні, алгебраїчні, механічні та інші докази.
Про відкриття теореми Піфагором складено багато різних легенд. Але, незважаючи на все це, ім'я Піфагора навіки увійшло в історію геометрії і міцно злилося з теоремою Піфагора. Адже цей геніальний математик першим представить доказ теореми, яка носить його ім'я.

формулювання теореми
Існують кілька формулювань теореми Піфагора.
Евклидова теорема говорить нам, що квадрат сторони прямокутного трикутника, проведений над його прямим кутом, дорівнює квадрату на сторонах, що містять прямий кут.
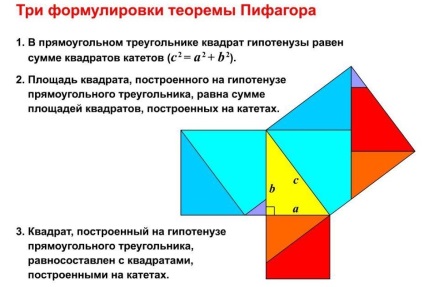
Завдання: Знайдіть різні формулювання теореми Піфагора. Чи знаходите ви в них якась відмінність?
Спрощене доведення Евкліда
Незалежно від того, ми беремо метод розкладання або доказ Евкліда, можна використовувати будь-яке розташування квадратів. У деяких випадках при цьому можна досягти невеликих спрощень.
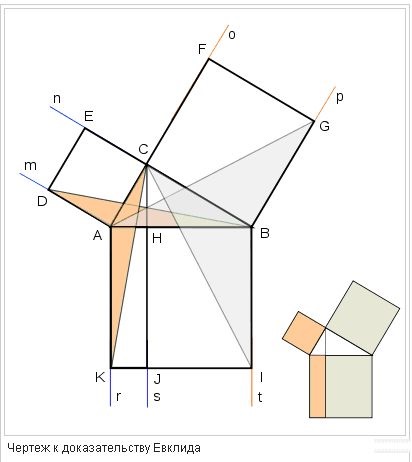
Візьмемо квадрат, який побудований на одному з катетів і має теж розташування, що і трикутник. Ми бачимо, що продовження боку, протилежного катета цього квадрата проходить через вершину квадрата, який побудований на гіпотенузі.
Доказ теореми виглядає досить просто, так як буде достатньо просто порівняти площі фігур з площею трикутника. І ми бачимо, що S трикутника дорівнює ½ площі квадрата, а також ½ S прямокутника.
Найпростіше доказ
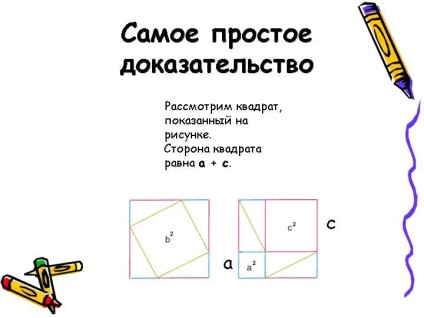
алгебраїчне доказ
До алгебраическому доведенню теореми Піфагора відносяться елементарні методи, які присутні в алгебрі. Це способи розв'язання рівнянь в поєднанні зі способом заміни змінних.
Давайте розглянемо це доказ більш детально. І так, у нас є прямокутник АВС, у якого прямий кут - С.
Проведіть з цього кута висоту CD.
Згідно визначення косинуса кута ми отримаємо:
соsА = AD / AC = AC / AB. Звідси AB * AD = AC2.
Тепер складемо ці рівності почленно і побачимо, що: AD + DB = AB,
Ось і все, теорема доведена.

Цікавий факт
Теорему Піфагора вчені «довели» за допомогою мультиків. Група однодумців з інституту ім. Стеклова отримала премію за оригінальний математичний проект, який вони розробили для школярів і вчителів. Вони створили міні уроки з математики, які цей нудний предмет перетворили в дуже цікавий і пізнавальний. Свої незвичайні етюди молоді вчені випустили на дисках і виклали в Інтернеті на загальний огляд.
1. Хто такий Піфагор?
2. Про що свідчить теорема Піфагора?
3. Які існують формулювання теореми Піфагора?
4. При вирішенні, яких завдань застосовується теорема Піфагора?
5. Де теорема Піфагора знайшла практичне застосування?
6. Які ви знаєте способи використання теореми Піфагора?
Завдання із застосуванням теореми Піфагора

Використовуючи знання теореми Піфагора, спробуйте вирішити такі завдання:
• З туристичної бази, одночасно, вийшли дві групи туристів. Перша група пішла на південь і пройшла сім кілометрів, а друга згорнула на захід і пройшла дев'ять кілометрів. Використовуючи знання теореми, знайдіть відстань між групами туристів.
• Якщо в прямокутному трикутнику його катет дорівнює 15 см, а гіпотенуза дорівнює 16 см, то чому дорівнює другий катет?
• Чому буде дорівнює площа трапеції, коли її велике основа дорівнює 24 см, менше - 16, а більша діагональ прямокутної трапеції дорівнює 26 см?

Домашнє завдання
Оформіть у вигляді невеликого доповіді кілька доказів теореми Піфагора, які вам зрозумілі і вирішите завдання.
1. Знайдіть діагональ прямокутного трикутника, за умови, що сторони його рівні 8 см і 32 см.
2. Знайдіть медіану трикутника, яка проведена до основи, якщо в трикутник периметр дорівнює 38 см, а його бічна сторона дорівнює 15 см.
3. У трикутника сторони рівні 10см, 6 см і 9 см. Спробуйте визначити, чи є цей трикутник прямокутним?