Теоретична і реальна міцність металу

еоретіческій розрахунок міцності кристала вперше був виконаний Я. Френкелем. В основу було покладено проста модель двох рядів атомів, які зміщуються відносно один одного під дією дотичного напруження т (рис. 5.1). При цьому передбачалося, що атоми верхнього ряду переміщуються щодо нижнього як одне ціле, одночасно. Такий механізм прийнято називати схемою жорсткого зсуву.

Теоретична і реальна міцність металу
На рис. 5.1. межплоскостное відстань (відстань між рядами) прийнято рівним а, а відстань між атомами в напрямку ковзання становить Ь. Під дією сдвигового напруги х атомні ряди будуть зміщуватися відносно один одного, потрапляючи в рівноважні позиції в таких точках, як А і В, де напруга зсуву, необхідне для збереження даної конфігурації, дорівнює нулю. Ця напруга дорівнює нулю також і в разі, коли в обох рядах атоми розташовуються точно друг над другом в положеннях С і D. У проміжних позиціях напруга має якісь кінцеві значення, які періодично змінюються в обсязі решітки. Якщо під дією сдвигового напруги зміщення становить х, то напруга буде періодичною функцією х з періодом'. У найбільш простій формі ця залежність може бути представлена ​​у вигляді синусоїдальної кривої (див. Рис. 5.1):
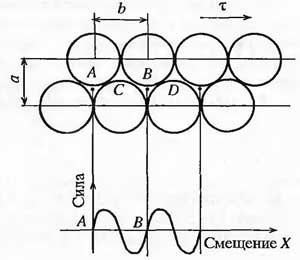
х = ksm (2nx / b). (5.1)

Для малих зсувів х = klnx / b. Використовуючи закон Гука, величину напруги зсуву можна уявити в іншому вигляді: т = Gx / a, де G - модуль зсуву; х / а - деформація зсуву.
Якщо прирівняти наведені вирази для х, то; х = Gb / lmi; підставляючи це значення х в співвідношення (5.1), отримаємо:
х = ksin (2nx / b)

Для малих зсувів х = klnx / b. Використовуючи закон Гука, величину напруги зсуву можна уявити в іншому вигляді: т = Gx / a, де G - модуль зсуву; х / а - деформація зсуву. Подальші розрахунки приводити не будемо.

Якщо прийняти, що а = Ь, тоді теоретичне критичне напруження зсуву приблизно дорівнює G / 2n. Наприклад, для кристалів міді G = 46 ТОВ МПа, отже, теоретичне значення т = 7320 МПа. У той же час для реальних кристалів міді спостерігається опір зрушенню становить всього лише 1,0 МПа. Таким чином, теоретичне значення міцності на кілька порядків вище дійсної величини.

Уточнення наведеного вище розрахунку шляхом використання більш близького до дійсності закону періодичної зміни т в залежності від х призводить до вираження ТКР = G / 30 (розрахунок по Маккензі), що також на кілька порядків перевищує реальний опір зрушенню.

Аналогічні міркування можна провести для випадку, коли в результаті дії нормальних напружень відбувається одночасний розрив міжатомних зв'язків для двох рядів атомів і утворюється тріщина. Робота, що витрачається на руйнування, витрачається на створення двох нових поверхонь, що володіють поверхневою енергією уг. Теоретичну міцність ідеального кристала, певну з умови рівності роботи відриву двох рядів атомів і поверхневої енергії, утвореної при цьому тріщини.

Фактична міцність матеріалів на кілька порядків менше значень теоретичної міцності. Пояснення розбіжності теоретичної і реальної міцності матеріалів дає теорія дефектів кристалічної будови, що дозволила розкрити сутність явищ, що відбуваються при пластичної деформації, і встановити фізичну природу пластичності і міцності металів і їх сплавів.

Схожі статті