Режими тертя і критерії розрахунку. Вище зазначено, що робота тертя є основним показником працездатності під-шіпніка. Тертя визначає знос і нагрівання підшипника, а також його ККД. Для зменшення тертя підшипники ковзання змазування вають. Залежно від режиму роботи підшипника в ньому може битьполужідкостное або рідинне треніе.Схематізірованное уявлення про ці режимах дає рис. 16.3.
При рідинному терті робочі поверхні вала і вкладиша розділені шаром масла, толщінаHкоторого більше суми висотRzшерховатостей поверхонь (на рис. 16.3 розділяє шар масла зображений товстою лінією):
При цьому умови масло сприймає зовнішнє навантаження, запобігаючи безпосереднє стикання робочих поверхонь-стей, т. Е. Їх знос. Опір руху в цьому випадку визна-ляется тільки внутрішнім тертям в шарі масла. Коефіцієнт рідинного тертя знаходиться в межах 0,001. 0,005 (що може бути менше коефіцієнта тертя кочення).
При напіврідинних терті умова (16.1) не дотримується, В підшипнику буде змішане тертя - одночасно рідинний-ве і граничне. Граничним називають тертя, при якому тертьових-еся поверхні покриті найтоншою плівкою масла, що утворила-ся в результаті дії молекулярних сил і хімічних реакцій активних молекул масла і матеріалу вкладиша. Здатність мас-ла до утворення граничних плівок (адсорбції) називають мас-
ляністостью (липкостью, змочують-мостью). Граничні плівки устої-чиви і витримують великі давши-лення. Однак в місцях сосредото-ченного тиску вони руйнуються, відбувається стикання чістихМасло Вкладишповерхностей металів, їх схвати-
Вання і відрив частинок матеріалу при відносному двіженіі.Полужід - Рис. 1б. з кісткове тертя супроводжується з-
Носом труться поверхностейдаже без попадання зовнішніх абразивних частинок. Коефіцієнт полужід-кісткового тертя залежить не тільки від якості масла, але також і від матеріалу, що труться. Для поширених анти-фрикційних матеріалів коефіцієнт напіврідинного тертя дорівнює 0,008. 0,1.
Для роботи підшипника найсприятливішим режимом є режим рідинного тренія.Образованіе режиму рідинного тертя є основним критерієм розрахунку більшості під-шіпніков ковзання. При цьому одночасно забезпечується ра-працездатність за критеріями зносу і заїдання.
Основи теорії рідинного тренія.Ісследованіе режиму рідинного тертя в підшипниках засноване на гідродинамічної теорії змащення. Ця теорія базується на рішеннях диференціювання альних рівнянь гідродинаміки в'язкої рідини, які зв'язок-ють тиск, швидкість і опір взякому зрушення.
На рис. 16.4 показані дві пластіниАі 27, залиті маслом і навантажені сілойF.ПластінаАдвіжется щодо пластини 27 з скоростьюVA.Еслі скоростьVAмала (рис. 16.4, а), то пластінаАвижімает масло з пластини 27. Поверхні пластин безпосередньо стикаються. При цьому утворюється полужід-кісткове тертя.
При досить великий скоростіVA (рис. 16.4, б) пластінаАподнімается в масляному шарі і приймає похиле положення, подібно до того, як піднімаються глісер або водні лижі, скільки-зящіе по воді.
Між пластинами утворюється звужує зазор, заповнений маслом, а рух відбувається в умовах рідинного тертя. Перехід до режиму рідинного тертя відбувається при деякій швидкості, званої крітіческойV ^. Розглянемо фізику цього явища.
"Основоположником цієї теорії є Н. П. Петров (1883). В подальшому ця теорія отримала розвиток в працях О. Рейнольдса, М. Є. Жуковського, С. А. ПАП-Лигин, А. Зоммерфельда, А. Мічел і ряду інших вчених.
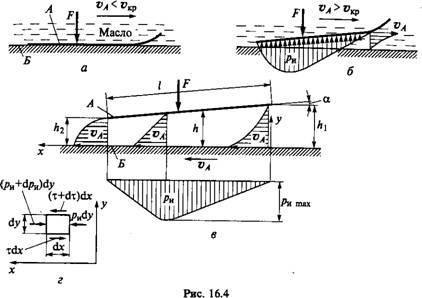
На рис. 16.4, б в одному з перерізів шару рідини в зазорі зображена епюра швидкостей рідини. У граничних точках шару швидкості рівні швидкостям пластінАіБ.Во всіх проміжних точках швидкості менше скоростіVAпластіниА. ПластінаАнабе-Гаета на рідину і проганяє її через звужується зазор. Цей процес буде ще ясніше, якщо розглянути звернене рух пластин. Для цього повідомимо всій системі зворотний рух зі скоростьюVA.Інтересующее нас відносний рух пластин при цьому не зміниться, але в зверненому русі пластінаАостановітся, а пластінаБбудет рухатися зі скоростьюVAв об-ратному напрямку (рис. 16.4, в). Епюри швидкостей в зверненому русі зображені на рис. 16.4, вдля декількох перетинів. Фор-ма цих епюр буде обгрунтована в подальшому за допомогою відпо-ціалу рівнянь. Тут у напрямку швидкостей ясно, як рідина запресовується під пластінуАі проганяється через зазор.
Покладемо далі, що ширина пластіниАсущественно більше її довжини / верб межі прямує до нескінченності. Це дозволяє знехтувати бічним плином рідини в зазорі і звести більш складну просторову задачу до плоскої з осях і у, со-зберігаючи цікавить нас фізику явища.
Основоположним є закон Ньютона
Де т - напруга зсуву від внутрішнього тертя при зсуві шарів рідини; Fi- динамічна в'язкість рідини, Па • с; V- ско-кість течії, м / с.
Закон Ньютона можна розглядати як аксіому, подібно до першого і другого його законам механіки. Фізичний сенс зако-ну можна пояснити так. Два тонких сусідніх шару мають некото-рую різницю швидкостей. На спільному кордоні шарів відбувається зрушення. Опір зрушенню пропорційно інтенсивності зміни швидкостей в поперечному напрямку або проізводнойdv / dy.Коеф-фициент пропорційності р залежить від властивостей рідини і визначається експериментально. Використовуючи цей закон, можна знайти все інші характеристики потоку рідини.
Продифференцировав рівняння Ньютона, отримаємо
Після підстановки отримаємо основне рівняння гідродинаміки для сталого двомірного течії рідини
Гдеh- поточна товщина шару масла в зазорі.
Об'ємна витрата на одиницю ширини пластини дорівнює
За умовою нерозривності потоку рідини велічінаQне повинна залежати отх (у всіх перетинах зазораQпостоянно). При цьому з рівняння (16.4) випливає, що градієнт давленіяGдолжен змінювати-ся зі зміною товщини слояhв відповідно до співвідношення
Рівняння (16.4) і (16.5) можна спростити, маючи на увазі, що на виході з пластини, де Л = Л2з надмірне давленіеря = 0. Так як постійний співмножник в рівнянні (16.5) не дорівнює нулю, прирівнюємо до нуля член в фігурних дужках при Л = Л2 і по-отримуємо
Підставляємо (16.6) в рівняння (16.5) і знаходимо
Це тиск масла в зазорі і врівноважує зовнішню нагрузкуF, а рух пластіниАпроісходіт при рідинному терті. Рівняння (16.7) дозволяє побудувати графік тиску (рис. 16.4, в). Максимум тиску зміщений до вузької сторони зазору.
Використовуючи отримані рішення, можна зробити наступні ви-води.
1.Так як расходQжідкості однаковий у всіх перетинах звужує-ющегося зазору, то середня швидкість течії повинна збільшуватися справа наліво (рис. 16.4, в). У той же час на кордонах з пластинами швидкості рідини постійні і рівні швидкостям пластин. У перетині, що збігається з максимумом тисків, dpjdx = -G = 0.Прі цьому, відповідно до рівняння (16.3), скоростьvв цьому перетині изменя-ється за лінійним законом пропорційно у. Тепер неважко зрозуміти, що, за умовою збільшення середньої швидкості справа нале-во, епюра в сеченііHбудет увігнутою, а в перетині й2 - опуклою. Величини швидкостей в будь-якому шарі і в будь-якому перетині можна розрахувати за рівнянням (6.3).
2. Встановити залежність тиску від товщини масляного шару. В середньому сеченііA = (AI + A2) / 2. При цьому після підстановки в (16.7) отримаємо
З огляду на малі величини зазорів (декілька мкм) і кута а, при-наближенні приймаємо й2 = 0 [6]. тоді
Отже, тиск обернено пропорційно товщині масляного шару. У підшипниках ця товщина має порядок деся-тих і сотих часток міліметра і тому тиск може до-Стігала дуже великих величин.
3. Якщо кут а нахилу пластіниАстремітся до нуля, то в межі будетh = h = h2і в рівнянні (16.7) отримаємо /? І = (00) / 0 = = 0. З цього випливає важливий висновок про те, що однією з умов освіти режиму рідинного тертя є наявність звужується зазору, який прийнято називати клі-новим.
У нашому прикладі початковий клиновий зазор утворюється за допомогою на-гою скошеної крайки пластини А. Якщо конструкція підшипника не має клинового зазору, то в підшипнику не може утворитися рідинне тертя. Наприклад, простий плоский подпятник (див. Рис. 16.1, б) не має клинового зазору і не може працювати при жид-кістковому терті. Для освіти клинового зазору, а слідчий-но, і умов рідинного тертя опорної поверхні підп'ятника надають спеціальну форму (див. Рис. 16.11).
У радіальних підшипниках клиновая форма зазору властива самій конструкції підшипників. Вона утворюється за рахунок зміщення центрів цапфи вала і вкладиша (ріс.16.S, а).
При кутовий скоростіш> Й), р цапфа спливає в маслі і не-скільки зміщується в бік обертання по траєкторії, зазначеної на рис. 16.5, б. На рис. 16.5, а, б: 1 клиновий зазор; 2 шлях центру цапфи при збільшенні швидкості обертання; 3 - епюра тиску в масляному шарі; 4 лінія центрів. З увеличени третьому кутової швидкості збільшується товщина розділяє мас-ляного шару Ащш, а центр цапфи зближується з центром вкладиша. Прісо-> оо відстань між центрами Повного совпаде-
Ня центрів бути не може, так як при цьому порушується клино-вая форма зазору, як одна з умов режиму рідинного тре-ня.
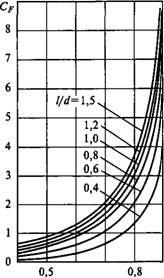
Дослідження показуючи-ють, що для підшипників з певними геометри-ними параметрами тол-щина масляного шару є-ється деякою функцією ха-рактеристики робочого ре-жиму підшипника