Презентація до уроку
Прямим круговим циліндром називається тіло, утворене обертанням прямокутника навколо свого боку.
Далі будемо називати це тіло циліндром.
Циліндр, утворений при обертанні прямокутника AOO1 A1 навколо боку OO1. яка називається віссю обертання (віссю циліндра) і є висотою циліндра. Підстави циліндра - рівні кола, розташовані в паралельних площинах. Висотою циліндра називають також відстань між площинами його основ. Відрізок, що з'єднує точки кіл підстав, перпендикулярний площин підстав, називається утворює циліндра (це, наприклад, відрізки A1 A. M1 M. B1 B. N1 N). Все що утворюють паралельні осі обертання і мають однакову довжину, рівну висоті циліндра. Радіусом циліндра називається радіус його заснування. Осьовим перерізом циліндра називається перетин циліндра площиною, що проходить через вісь обертання. Всі осьові перетину циліндра - рівні прямокутники (це, наприклад, прямокутники ABB1 A1 і MNN1 M1).
Площина, що містить утворить і перпендикулярна осьового перерізу, що проходить через цю твірну, називається дотичній до циліндра площиною. Утворює циліндра при обертанні навколо осі утворює бічну (циліндричну) поверхню циліндра.
На рис. 5.2 показана розгортка циліндра. Розгорткою бічній поверхні циліндра є прямокутник зі сторонами H і C. де H - висота циліндра, а C - довжина кола основи.
Наведемо формули для обчислення площ бічної Sб і повної Sn поверхонь
Прямим круговим конусом називається тіло, утворене при обертанні прямокутного трикутника навколо катета.
Далі прямий круговий конус будемо називати просто конусом.
Конус, утворений внаслідок обертання прямокутного трикутника POA навколо катета PO, званого віссю конуса, P називається вершиною конуса. Коло з центром O і радіусом OA називається підставою конуса. Відрізок, що з'єднує вершину конуса з якою - небудь точкою кола підстави називається твірною конуса. На рис. 5.3 відрізки PA, PB, PM, PN - утворюють конуса. Радіус основи конуса називається радіусом конуса. Висотою конуса називається перпендикуляр, опущений з вершини конуса на його підставу. Осьовим перерізом конуса називається перетин конуса площиною, що проходить через його висоту.
Площина, що проходить через творчу конуса і перпендикулярна осьового перерізу, що проходить через цю твірну, називається дотичній площиною конуса. При обертанні утворює PA навколо осі PO утворюється бічна (конічна) поверхню конуса.
Розгорткою бічній поверхні конуса є кругової сектор.
Позначимо через Sб і Sn відповідно площі бічної і повної поверхні конуса:, де - кут при вершині розгортки. Далі зауважимо, що. Отже,, де R - радіус, а l - утворює конуса;
Усічений конус
Усіченим конусом називається частина конуса, обмежена його підставою і перетином, площина якого паралельна площині підстави.
Утворює і висота усіченого конуса є частинами утворює і висоти повного конуса.
Бічна поверхня усіченого конуса може бути знайдена за формулою: Sб = (R + r) l, де R і r - радіуси підстав, l - утворює конуса.
Повна поверхня знаходиться за формулою: Sn = (Rl + rl + R 2 + r 2).
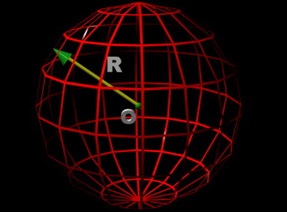
Безліч всіх точок простору, однаково віддалених на відстань R від даної точки O. називається сферою.
Сферу позначають так: (O, R). Можна визначити сферу і як тіло, утворене при обертанні кола навколо свого діаметра.
Безліч всіх точок простору, віддалених від даної точки O на відстань, що не більше R. називається кулею.
Іншими словами куля - це об'єднання сфери і всіх її внутрішніх точок.
Можна також визначити куля і як тіло, утворене при обертанні кола навколо свого діаметра.
Куля позначають також як сферу: (O, R). Точка O називається центром сфери (кулі). Відрізок, що з'єднує центр сфери з будь-якій її точкою, називається радіусом сфери (кулі). Відрізок, що з'єднує будь-які дві точки сфери, називається хордою сфери (кулі). Іноді під радіусом або хордою увазі їх довжину. Хорда, що проходить через центр сфери, називається її діаметром.
Т1. Якщо відстань від центру сфери до площини менше радіуса сфери, то лінія перетину сфери цієї площиною - коло.
З теореми випливає, що, коли відстань від центру кулі до площини менше радіуса, перетин кулі цією площиною - коло. Якщо площину віддалена від центру сфери на відстань R. то вона називається дотичній площиною.
Т2. Касатльная площину має зі сферою єдину спільну точку (точку дотику) і перпендикулярна радіусу, проведеного в точку дотику.
Т3. Площині, рівновіддалені від центру сфери, перетинають її по рівним колах.
Доказ випливає з того, що, де r - радіус лінії перетину.
Ясно, що найбільша окружність утворюється при перетині площиною, що проходить через центр сфери. Лінія перетину називається великою окружністю сфери. (Відповідне перетин кулі називається великим колом кулі).
Пряма, проведена через точку сфери перпендикулярно радіусу, проведеного в цю точку, називається дотичною прямою до сфери.
Т4. Дотична сфери має зі сферою єдину спільну точку.
Через будь-яку точку сфери можна провести нескінченне число дотичних прямих, причому всі вони лежать в дотичній площині.
Нехай O (a; b; c) - центр сфери в декартовій системі координат, R - радіус сфери, A (x; y; z) - довільна точка сфери. (Дивись координат на чолі 8.) Тоді
Ми отримали рівняння сфери з центром O (a; b; c) і радіусом R.
Зокрема, якщо центром сфери є початок координат, то маємо рівняння x 2 + y 2 + z 2 = R 2.
Зауважимо, що куля задається нерівністю