Цю сторінку пропонується об'єднати з Точка Ферма.
Точки Торрічеллі - дві точки, з яких всі сторони трикутника видно або під кутом в 60 °, або під кутом в 120 °. Ці точки в трикутнику - «парні». Іноді ці точки називають точками Ферма або точками Ферма-Торрічеллі.
- Дві Точки Торрічеллі - це точки перетину:
- c відповідними вільними вершинами рівносторонніх трикутників. побудованих на сторонах трикутника (назовні) - перша точка Торрічеллі
- з відповідними вільними вершинами правильних трикутників, побудованих всередину трикутника - друга точка Торрічеллі.
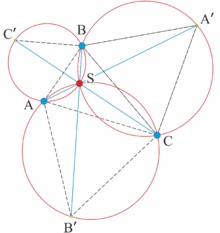
Побудова точки Торрічеллі для трикутників з кутами, що не перевершують 120 °.
Цитата з П. Ферма: "Datis tribus punctis, quartum reperire, a quo si ducantur tres rectæ ad data puncta, summa trium harum rectarum sit minima quantitas". P. de Fermat, «Œuvres de Fermat», тисяча шістсот сімдесят дев'ять, Livre I, Paris. (Лат. "Для трьох заданих точок знайти четверту, таку що якщо від неї провести прямі лінії до даних точок, сума відстаней буде найменшою". П. Ферма ).
- Перша точка Торрічеллі має найменшу суму відстаней до вершин трикутника.
- Перша точка Торрічеллі - точка трикутника. з якої всі сторони видно під кутом в 120 °. Вона існує тільки в трикутниках з кутами меншими 120 °, при цьому, вона єдина і, отже, збігається з точкою Ферма.
- Перша точка Торрічеллі - окремий випадок точки Ферма. існуючої в будь-якому трикутнику.
- Дві точки Торрічеллі і точка Лемуана лежать на одній прямій.
- Точки Торрічеллі ізогонально пов'язані точкам Аполлонія
- Побудуємо дві прямі, кожна з яких проходить через точку Аполлонія і точку Торрічеллі, відмінну від ізогонально сполученої їй. Такі прямі перетнуться в точці перетину медіан (в центр ваги трикутника).
- Теорема Лестера [1]. У будь-якому різнобічному трикутнику дві точки Торрічеллі, центр дев'яти точок і центр описаного кола лежать на одному колі (окружності Лестера).
Гіпербола Киперта - описана гіпербола, що проходить через центр ваги і Ортоцентр. Якщо на сторонах трикутника побудувати подібні трикутник (назовні або всередину), а потім з'єднати їх вершини з протилежними вершинами вихідного трикутника, то три таких прямі перетнуться в одній точці, що лежать на гіперболі Киперта. Зокрема, на цій гіперболи лежать точки Торрічеллі і точки Наполеона (точки перетину чевіан, що з'єднують вершини з центрами побудованих на протилежних сторонах правильних трикутників) [2].
До речі, на першому малюнку справа центри трьох рівносторонніх трикутників самі є вершинами нового рівностороннього трикутника (Теорема Наполеона). Крім того, AA '= BB' = CC '.