Якщо оцінка параметра є одним число, таку оцінку називають точковою (це точка на числовій осі). Розглянуті вище оцінки є точковими.
Якщо при оцінюванні ми знаходимо інтервал значень, в який істинне значення потрапляє з певною ймовірністю, то така оцінка буде інтервального. Відповідний інтервал називаютдоверітельним інтервалом. а ймовірність -доверітельной ймовірністю (ілінадежностью).
Наприклад, нехай x- середній бал студента.
Приклад точкової оцінки: = 4,5.
Приклад інтервального оцінки: 4,2 ≤ ≤ 4,8 (або, що те ж саме, = 4,5 ± 0,3) з ймовірністю 0,93. Інший приклад інтервального оцінки: 4,1 ≤≤ 4,9 з імовірністю 0,95 (тобто = 4,5 ± 0,4).
Слід звернути увагу, що чим більше береться довірча ймовірність, тим ширше виявляється довірчий інтервал. Власне, в наведеному прикладі, навіть не знаючи значення середньої, можна точно сказати (з ймовірністю 1), що 2 ≤ ≤ 5, так як інших значень оцінка в цій шкалі прийняти взагалі не може. Однак така інформація очевидно марна для дослідника. Чим менше береться довірчий інтервал, тим більша ймовірність помилки, тобто того, що ми в нього не потрапимо (а довірча ймовірність, відповідно, менше). Тобто більш точні оцінки даються з меншою ймовірністю.
Отже, якщо межі довірчого інтервалу для значень деякого параметра А визначаються формулою А ± прі довірчої вероятності, то чим больше, тим больше. Для определеніяіспользуются формули, вид яких залежить від того, який параметр оцінюється, яким методом, і вибірка якого типу при цьому використовується. Крім того, при расчетепо цими формулами використовується інформація про обсяги вибірки і генеральної сукупності і про значеніі. Необхідні формули можна знайти в підручниках і довідниках по статистиці.
Перевірка статистичних гіпотез
Статистична гіпотеза - це будь-яке припущення про вид або про значення параметрів імовірнісного розподілу.
При перевірці статистичних гіпотез ту гіпотезу, яку перевіряють, прийнято називати нульовий гіпотезою і обозначатьHо. Одночасно рассматріваютальтернатівную (конкуруючу) гіпотезу Н1. ГіпотезиHо і Н1 повинні бути протилежні одна одній.
Принцип перевірки статистичних гіпотез полягає в наступному. На основі вибірки даних розраховують якийсь показник , який називають статистикою критерію. Цей показник є випадковою величиною (оскільки він розраховується за вибіркою), але його вибирають таким чином, що його імовірнісний розподіл відомо (можливо, наближено). Крім того, значеніедолжно бути пов'язано з тим, виконується чи ні перевіряється гіпотеза. Всі можливі значеніяразбівают на дві непересічні області -область прийняття гіпотези ікрітіческую область (в якій гіпотеза відхиляється). Наприклад, вибирають критичне значення статистики крітеріякр таке, що якщо гіпотеза вірна, то ймовірність α перевищити це значення α = Р (> кр) дуже мала (α = Р (> кр)). Тоді прі≤кр гіпотеза приймається, а при всіх інших значеніяхотклоняетсяHо.
Правило перевірки статистичної гіпотези називають статистичним критерієм.
Однак, з імовірністю α може бути все ж допущена помилка (тобто гіпотеза Але буде відкинута, хоча насправді вона правильна). Це може статися тому, що значення статистики потрапило в критичну область випадково. Таку помилку називаютошібкой першого роду. а відповідну ймовірність називаютуровнем значимості критерію. Вона повинна бути невеликою.
Крім того, може бути допущена також помилка другого роду : вона полягає в тому, що гіпотезаHо приймається, хоча насправді вона є невірною (а вірна альтернативна гіпотезаH1). Відзначимо, що під час перевірки однієї і тієї ж гіпотези за вибіркою одного і того ж обсягу неможливо одночасно зменшити ймовірність помилок першого і другого роду. Це пов'язано з тим, що з ростом критичної області одночасно зростають і α, і. Адже чим більше критична область, тим більша ймовірність відхилити гіпотезу і менше ймовірність її прийняти (відповідно, більша ймовірність відхилити вірну або прийняти невірну). Імовірність НЕ допустити помилку другого роду називаетсямощностью критерію (вона дорівнює 1 -).
Одночасно збільшити потужність критерію і зменшити рівень значимості можна тільки за рахунок збільшення обсягу вибірки, тому що тільки за цієї умови вибіркові значення показників будуть більш точно відображати дійсні характеристики розподілу, а ймовірність випадкових відхилень зменшиться.
Наприклад, на склад надійшла партія виробів. З неї відбирають частину виробів для перевірки на шлюб. За результатами перевірки буде прийнята або відкинута нульова гіпотеза, яка полягає в наступному: частка бракованих виробів в партії невелика, і партію можна прийняти. Припустимо спочатку, що в обраних виробах частка бракованих була велика, і за результатами вибіркового контролю всю партію забракували. Однак, є ймовірність, що перевіряючому випадково попалися саме погані вироби, і насправді партію треба було прийняти, тому що інші вироби не містять шлюбу. В цьому випадку була допущена помилка першого роду, тобто відхилили вірну нульову гіпотезу (відкинули хороші вироби). Тепер припустимо, що в обраних виробах частка бракованих була невелика, і за результатами вибіркового контролю партію прийняли. Однак, є ймовірність, що перевіряючому випадково попалися саме хороші вироби, і насправді партію треба було забракувати. В цьому випадку була допущена помилка другого роду, тобто прийнята невірна нульова гіпотеза. З наведених прикладів видно, що чим більше виробів буде вибрано для перевірки, тим менше ризик зробити і ту, і іншу помилку. При рівному обсязі вибірки чим суворіше критерії перевірки (більше критична область), тим більша ймовірність припуститися помилки першого роду і менше - другого (і навпаки).
У юріспуденціі під нульовий гіпотезою зазвичай мається на увазі гіпотеза про те, що підсудний невинний. Відповідно, помилка першого роду - це звинувачення невинного, а помилка другого роду - це виправдання винного. Завдання низького рівня значущості означає, що ймовірність помилки першого роду повинна бути маленькою, тобто ризик прийняти невірне, «звинуватити невинного» повинен бути маленьким.
Залежно від виду критичної області все статистичні критерії прийнято ділити на три основні класи. Розглянемо їх на прикладі, в якому статистика імеет стандартний нормальний розподіл (т.е. = N (0; 1)) і заданий п'ятивідсотковий рівень значущості (α = 0,05):
1) правобічна критична область задається нерівністю
Якщо α = 0,05, то площа під графіком щільності стандартного нормального розподілу праворуч від прямої х = кр повинна становити 0,05. Вся площа під цим графіком праворуч від вертикальної осі становить 0,5. Щоб знайти значеніекр. скористаємося функцією Лапласа, яка повинна тут прийняти значення 0,5 - 0,05 = 0,45. Таке значення соответствуеткр = 1,64.
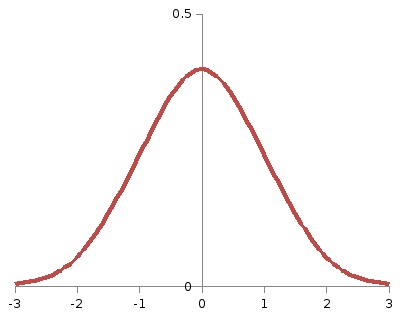
На малюнку 20 площа заштрихованої фігури становить 0,05, тобто 5% від одиниці (від загальної площі графіка під функцією щільності ймовірності). Це означає, що Р (> кр) = α = 0,05. З такою ймовірністю перевіряється гіпотеза буде все-таки відкинута, навіть якщо вона насправді вірна. Якщо фактичне значення статистики крітерія≤кр. гіпотеза приймається.
2) лівостороння критична область задається нерівністю
Таке значення відповідає кр = -1,64. На малюнку 21 площа заштрихованої фігури також становить 0,05, тобто Р (<кр ) = α = 0,05. Если фактическое значение статистики критерия≥кр. гипотеза принимается.
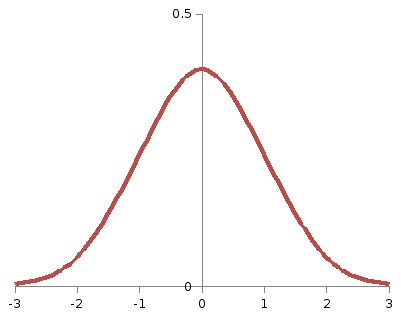
3) двостороння критична область задається нерівностями
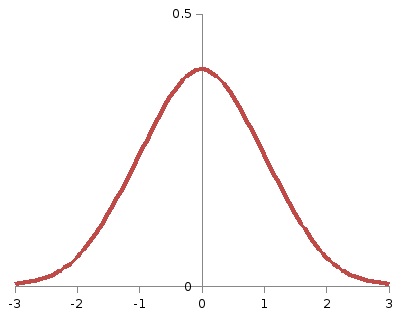
Оскільки площа під графіком щільності розподілу в критичній області повинна складати 0,05, площа кожного з двох заштрихованих ділянок на малюнку 22 повинна становити 0,025 (тобто α / 2). Тоді функція Лапласа при х = кр2 повинна прийняти значення 0,5 - 0,025 = 0,475. Таке значення соответствуеткр2 = 1,96. Відповідно, кр1 = -1,96.
Отже, при використанні двостороннього критерію Р (<кр1 ) = = Р(>кр2) = α / 2. Еслікр1 ≤≤кр2. гіпотеза приймається.
Розглянемо наступний приклад. Машина для розфасовки спецій при поставці була відрегульована так, щоб середня маса спецій в пакетику в пробної партії з 50 штук становила 0 = 90 (г) при СКОх = 10 (г). З розфасованої через місяць партії було відібрано 60 пакетиків, і середня маса спецій в пакетику составіла0 = 86 (г) при СКОy = 8,5 (г). Необхідно з'ясувати, чи є це випадковим збігом, або регулювання машини порушена.
Сформулюємо нульову гіпотезу: регулювання не порушена. Це означає, що насправді середні величини при постачанні і зараз рівні, тобто М (-) = М () - М () = 0. Будемо вважати, що випадкова величина-має нормальний розподіл з математичним очікуванням 0.
Знайдемо СКО цієї випадкової величини.
Яка дисперсія випадкової величини? D () = D ((xi) / n)) = = (D (xi)) / n 2 = (D (xi)) / n 2 = 2 х * n / n 2 = 2 х / n, гдеn = 50, т.е.D () = 100/50 = 2.
Аналогічно D () = 2 y / n, гдеn = 60, т.е.D () = 8,5 2/60 = 72,25 / 601,2.
Тоді D (-) = D () + D () = 3,2, а СКО1,79.
Тоді статистика = (-) / 1,79 матиме стандартний нормальний розподіл, т.е. = N (0, 1). Взявши в якості оцінок генеральних середніх вибіркові оценкі0 і0. розрахуємо фактичне значення статистики критерію: = () / 1,792,23.
Задамося рівнем значимості 5%. Побудуємо двосторонню критичну область: якщо фактичний критерій потрапляє в неї, то це означає, що різниця між середніми занадто істотно відрізняється від нуля в ту або іншу сторону; і тоді гіпотезу про рівність середніх треба відкинути. По таблиці функції Лапласа знайдемо межі цієї області: Ф (кр2) = 0,5 - 0,05 / 2 = 0,475, тогдакр2 = 1,96; кр1 = -1,96. Так як 2,23> 1,96, гіпотеза Н0 відкидається, тобто регулювання машини порушена. Однак, існує п'ятивідсоткова ймовірність, що цей висновок зроблений випадково (тобто насправді з машиною все в порядку, просто були зроблені невдалі вибірки).
Задамося рівнем значущості 2%. Тоді кордону критичної області знайдемо по таблиці функції Лапласа для значення цієї функції Ф (кр2) = 0,5 - 0,02 / 2 = 0,49, тоді тогдакр2 = 2,34; кр1 = -2,34. Так як 2,23> 2,34, на двопроцентному рівні значущості можна прийняти нульову гіпотезу. Тобто вважати, що регулювання машини не порушена.