Основні поняття теорії графів
Топологічних ОПИС СХЕМ
Під математичною моделлю розуміють сукупність рівнянь, що описують ланцюг, рішення яких дозволяє визначити її характеристики. В якості математичних моделей зазвичай виступають системи лінійних, нелінійних алгебраїчних або диференціальних рівнянь. В основі методів формування математичних моделей ланцюгів лежить сукупність топологічних і компонентних рівнянь.
Топологію схем зручно описувати на мові теорії графів, що має безліч інженерних додатків. Топологія схеми несе інформацію про з'єднання елементів. Топологічні рівняння ланцюга є формою запису основних топологічних законів (перший і другий закони Кірхгофа). Компонентні рівняння являють собою запис законів Ома для компонентів - елементів схеми.
Для опису топології ланцюга кожен двополюсний елемент заміщається спрямованим відрізком лінії, званим гілкою графа. З'єднання двох і більше гілок в точці називається вузлом або вершиною графа. Пронумеруємо гілки і вузли електричної схеми та відповідного їй графа.
Сформулюємо закони Кирхгофа для електричних ланцюгів.
Закон Кірхгофа для напруг: сума падінь напруг уздовж будь-якого замкнутого контуру ланцюга дорівнює нулю.
Закони Кірхгофа для струмів:
1. Алгебраїчна сума струмів, що втікають у вузол і що випливають із вузла, дорівнює нулю.
2. У будь-якому перетині, що розділяє ланцюг на дві частини, алгебраїчна сума струмів, що протікають по з'єднувальним гілкам через перетин, дорівнює нулю.
Напрямки відрізків ліній (струмів) пасивних гілок можна вибирати довільно, однак домовимося, що для джерел струму напрямок збігається з істинним, а для джерел напруги направлено проти ЕДС.Узли схеми нумеруються в довільному порядку безперервної послідовністю цифр, загальний (заземлений вузол) зазвичай вважається нульовим .
Матриця інціденцій. Застосування закону Кирхгофа для струмів в вузлах дозволяє отримати матрицю інціденцій, яка буде показувати топологічні властивості ланцюга. Розглянемо просту ланцюг і відповідний їй граф (рисунок 2.1).
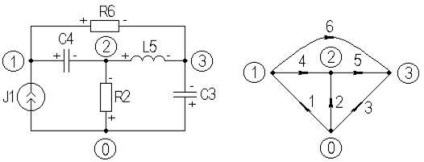
Малюнок 2.1 - Електричне коло і її спрямований граф
Запишемо закон Кірхгофа для струмів у вузлах:
Етіуравненія можна записати в матричній формі
де - матриця інціденцій.
Для розглянутого прикладу матриця має вигляд:
Матриця містить рядків і стовпців, де - число незалежних (незаземленій) вузлів; - число гілок графа. Рядки матриці вказують гілки, інцідентние відповідного вузла, і їх спрямованість. Стовпці матриці вказують вузли, інцідентние відповідної гілки і порядок обходу.
Напруги гілок і вузлові потенціали також пов'язані через матрицю інціденцій співвідношенням, що відповідає закону Кирхгофа для напруг
де - транспонована матриця інціденцій; - напруга гілок, - напруги вузлів.
Матриці перетинів і контурів. Зобразимо на рисунку 2.2 граф попередньої ланцюга, але з трьома перетинами. Позитивний напрямок перетинів вкажемо стрілками.
Малюнок 2.2 - Граф схеми з перетинами
Складемо рівняння для струмів перетинів:
Виникає питання: скільки необхідно мати рівнянь для визначення всіх струмів і напруг ланцюга? Для відповіді слід скористатися поняттям дерева графа.
Деревом пов'язаного графа називається пов'язаний підграф, що включає всі вузли графа, але не містить замкнутих контурів. Гілки, що не увійшли в дерево графа, утворюють додаток дерева графа. Дерево графа ланцюга з () вузлами має гілок. Гілки графа, що входять в дерево, називаються ребрами. Гілки доповнення графа називаються хордами.
Головним перетином графа називають перетин, що проходить через одне ребро і довільне число хорд. Оскільки в дерево входить тільки гілок, то існує головних перетинів, що відповідає незалежним рівнянням для струмів.
Нумерація гілок і вузлів схеми представляє довільну процедуру і диктується міркуваннями зручності. Багато викладки істотно спростяться, якщо:
1) вибираємо напрямки гілок;
2) вибираємо дерево графа;
3) нумеруем гілки графа, спочатку ребра, потім хорди.
На малюнку 2.3 зображений один з варіантів такого вибору. Рівняння для струмів перетинів в цьому випадку будуть наступними:
Малюнок 2.3 - Граф схеми з виділеним деревом
У матричної формі ці рівняння можна записати у вигляді