Перестановка порядку n це биективное відображення кінцевого безлічі з n елементів в себе.
&space;1&space;&space;2&space;3&space;4 # 92; # 92;&space;2&space;&space;413&space;# 92; end "/>, що означає перестановку,Також можна для зручності переставляти стовпці місцями:
Для наочності, ту ж перестановку можна зобразити картинкою виду
Приклад обчислення добутку перестановок. якщо
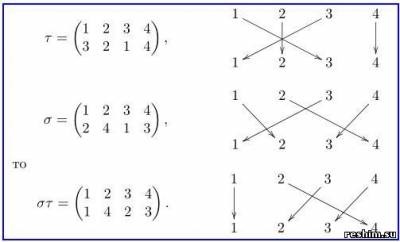
За допомогою звичайного визначення зручно обчислювати твір так: в перестановці σ переставляємо стовпці так, що перший рядок в σ збігається з останнім рядком в τ. Тоді твором буде перестановка, у якій перший рядок - стандартна, а другий рядок - це другий рядок з σ.
Приклад 2. Знайти твір перестановок можна і так
Перша перестановка переводить один в два, а друга два в сім, значить твір переводить один в сім і т.д.
Перестановки зручно перемножать і в тому випадку, коли вони представлені у вигляді добутку непересічних циклів.
Наприклад: στ = (1,2,4,3) · (1,3) = (2,4,3)
При цьому твір виходить так: для кожного елемента від 1 до 4 треба пройти по циклам в лівій частині і простежити куди він переходить.
Зокрема, 3 спочатку переходить в 1 (цикл (1. 3)),
а потім 1 в 2 (цикл (1. 2. 4. 3)).
Значить в творі 3 буде переходити в 2.
Множення перестановок некомутативними: τσ ≠ στ.
Отже рішення рівнянь виду: τx = σ, xτ = σ
x = τ -1 σ, x = στ -1