Визначення [| ]
Еліпс - геометричне місце точок M евклідової площини. для яких сума відстаней до двох даних точок F 1> і F 2> (званих фокусами) є сталою і більше відстані між фокусами, тобто
Пов'язані визначення [| ]
- Проходить через фокуси еліпса відрізок AB, кінці якого лежать на еліпсі, називається великий віссю даного еліпса. Довжина великої осі дорівнює 2 a у вищенаведеному рівнянні.
- Відрізок CD, перпендикулярний великої осі еліпса, що проходить через центральну точку великий осі, кінці якого лежать на еліпсі, називається малою віссю еліпса.
- Точка перетину великої і малої осей еліпса називається його центром.
- Відрізки, проведені з центру еліпса до вершин на великій і малій осях називаються, відповідно, велика піввісь і малої півосі еліпса, і позначаються a і b.
- Відстані r 1> і r 2> від кожного з фокусів до даної точки на еліпсі називаються фокальними радіусами в цій точці.
- Відстань c = | F 1 F 2 | 2 F_ | >>> називається фокальним відстанню.
- Величина e = c a = 1 # X2212; b 2 a 2> = >>>>>> називається ексцентриситетом.
- Діаметром еліпса називають довільну хорду, що проходить через його центр. Сполученими діаметрами еліпса називають пару його діаметрів, що володіють наступною властивістю: середини хорд, паралельних першому діаметру, лежать на другому діаметрі. В цьому випадку і середини хорд, паралельних другого діаметру, лежать на першому діаметрі.
- Радіус еліпса в даній точці це відрізок, що з'єднує центр еліпса з точкою, а також його довжина, яка обчислюється за формулою r = a b b 2 cos 2 # X2061; # X03C6; + A 2 sin 2 # X2061; # X03C6; = B 1 # X2212; e 2 cos 2 # X2061; # X03C6; \ Cos ^ \ varphi + a ^ \ sin ^ \ varphi >>> = \ cos ^ \ varphi >>>>. де # X03C6; - кут між радіусом і велика піввісь.
- Фокальним параметром p = b 2 a >>> називається половина довжини хорди. що проходить через фокус і перпендикулярній великий осі еліпса.
- Відношення довжин малої і великої півосей називається коефіцієнтом стиснення еліпса або еліптичності. k = b a.>.> Величина, рівна (1 # X2212; k) = a # X2212; b a.>,> називається стисненням еліпса. Для окружності коефіцієнт стиснення дорівнює одиниці, стиснення - нулю. Коефіцієнт стиснення і ексцентриситет еліпса пов'язані співвідношенням k 2 = 1 # X2212; e 2. = 1-e ^.>
- Для кожного з фокусів існує пряма, яка називається директоркою. така, що відношення відстані від довільної точки еліпса до його фокусу до відстані від цієї точки до даної прямої дорівнює ексцентриситету еліпса. Весь еліпс лежить по ту ж сторону від такої прямої, що і фокус. Рівняння директрис еліпса в канонічному вигляді записуються як x = # X00B1; p e (1 + e) >> для фокусів ( # X2213; p 1 + e. 0)>, \, 0 \ right)> відповідно. Відстань між фокусом і директоркою одно p e.>.>
Співвідношення між елементами еліпса [| ]
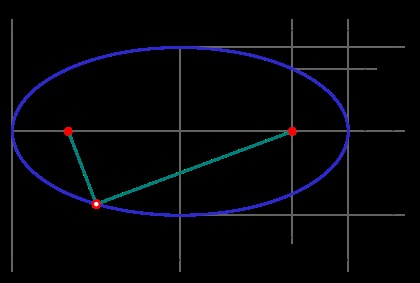
Частини еліпса (опис див. В розділі «Пов'язані визначення»)
Еліпс як крива другого порядку [| ]
Еліпс є центральною невироджених кривої другого порядку і задовольняє загальним рівнянням виду
a 11 x 2 + a 22 y 2 + 2 a 12 x y + 2 a 13 x + 2 a 23 y + a 33 = 0. x ^ + a_y ^ + 2a_xy + 2a_x + 2a_y + a_ = 0,>
Співвідношення між інваріантами кривої другого порядку і півосями еліпса (вірно тільки за умови, що центр еліпса збігається з початком координат і a 33 = # X2212; 1 = -1>):
Якщо переписати загальне рівняння у вигляді
A X 2 + B X Y + C Y 2 + D X + E Y + F = 0. + BXY + CY ^ + DX + EY + F = 0,>
то координати центру еліпса:
кут обертання визначається з виразу
Напрями векторів осей:
Довжини півосей визначаються виразами
Зворотне співвідношення - коефіцієнти загального рівняння з параметрів еліпса - можна отримати, підставивши в канонічне рівняння (див. Розділ нижче) вираз для повороту системи координат на кут Θ і перенесення в точку (x c. Y c), y _)>:
x # X2032; 2 a 2 + y # X2032; 2 b 2 = 1 >>> + >>> = 1> x # X2032; = (X # X2212; x c) c o s # X0398; + (Y # X2212; y c) s i n # X0398; ) Cos \ Theta + (y-y_) sin \ Theta> y # X2032; = # X2212; (x # X2212; x c) s i n # X0398; + (Y # X2212; y c) c o s # X0398; ) Sin \ Theta + (y-y_) cos \ Theta>
Виконавши підстановку і розкривши дужки, отримаємо такі вирази для коефіцієнтів загального рівняння:
A = a 2 (s i n # X0398; ) 2 + b 2 (c o s # X0398; ) 2 (sin \ Theta) ^ + b ^ (cos \ Theta) ^> B = 2 (b 2 # X2212; a 2) s i n # X0398; c o s # X0398; -a ^) sin \ Theta cos \ Theta> C = a 2 (c o s # X0398; ) 2 + b 2 (s i n # X0398; ) 2 (cos \ Theta) ^ + b ^ (sin \ Theta) ^> D = # X2212; 2 A x c # X2212; B y c -By_> E = # X2212; B x c # X2212; 2 C y c -2Cy_> F = A x c 2 + C y c 2 + B x c y c # X2212; a 2 b 2 ^ + Cy _ ^ + Bx_y_-a ^ b ^>
Якщо ввести тільки кут, а центр еліпса залишити на початку координат, то
Слід зауважити, що в рівнянні загального вигляду еліпса, заданого в Декартовой системі координат, коефіцієнти ABCDE F (або, що те ж саме, a 11. 2 a 12. a 22. 2 a 13. 2 a 23. a 33, 2a_, a_, 2a_, 2a_, a_>) є певними з точністю до довільного постійного множника, тобто наведена вище запис і
A k X 2 + B k X Y + C k Y 2 + D k X + E k Y + F k = 0 + BkXY + CkY ^ + DkX + EkY + Fk = 0>
де k # X2260; 0. є еквівалентними. Не можна очікувати, що вираз
буде виконано при будь-якому k.
Співвідношення між інваріант I і півосями в загальному вигляді виглядає наступним чином:
де F # X2032; = F # X22C5; (A # X22C5; h 2 + B # X22C5; h # X22C5; k + C # X22C5; k 2 # X2212; 1) + B \ cdot h \ cdot k + C \ cdot k ^ -1)> - коефіцієнт F при перенесенні початку координат в центр еліпса, коли рівняння приводиться до вигляду
Інші інваріанти знаходяться в таких пропорціях:
Канонічне рівняння [| ]
Для будь-якого еліпса можна знайти декартову систему координат таку, що еліпс буде описуватися рівнянням:
Це рівняння називається канонічним рівнянням еліпса. Воно описує еліпс з центром на початку координат, осі якого збігаються з осями координат. [1]
Для визначеності покладемо, що 0
Знаючи піввісь еліпса можна обчислити його фокальное відстань і ексцентриситет:
Координати фокусів еліпса:
Еліпс має дві директриси, рівняння яких можна записати як
Фокальний параметр (т. Е. Половина довжини хорди. Проходить через фокус і перпендикулярній осі еліпса) дорівнює
Фокальні радіуси, т. Е. Відстані від фокусів до довільної точки кривої (x. Y).
Рівняння діаметра. сполученого хордам з кутовим коефіцієнтом k. :
Рівняння дотичної до еліпса в точці (x 0. y 0), y _)> має вигляд.
Рівняння дотичних, що мають даний кутовий коефіцієнт k:
точки дотику такої прямої еліпса (або що те ж саме, точки еліпса де дотична має кут з тангенсом k):