Мета. систематизувати, узагальнити знання учнів; знати формули обчислення площі кола, довжини кола; вміти використовувати формули для обчислення і вирішення нестандартних завдань; користуватися креслярськими інструментами; прищепити любов до геометрії, розвинути творче ставлення до справи; збагатити історичні знання в галузі геометрії.
Обладнання: кодоскоп, кольорові гуртки різного діаметру, історичні картини, роздатковий матеріал.
План уроку:- Організаційний момент.
- Розминка: а) бліц-опитування; б) формули, робота з малюнками; в) робота з кодоскоп (тест).
- Вирішення задач.
- Практична робота.
- Окружність в архітектурі і в народній творчості.
- З історії…
- Підсумок уроку.
- Домашнє завдання.
(На дошці за картками заховані слова. На самих же картках ці слова зашифровані у вигляді плутанини букв.)
Учитель: Хлопці! Відгадайте зашифровані слова.
Учитель. Сьогодні тема: «Це чудове коло!». Саме коло. Серед кривих ліній вона найдивовижніша. Окружність - замкнута лінія. Частина площини, обмеженою нею - це добре відомий вам коло.
Мета нашого уроку з вами: повторити формули обчислення площі кола, довжини кола; застосувати формули для вирішення різних нестандартних завдань і з'ясувати, чим так чудова окружність.
Учитель: Проведемо розминку. Я буду починати речення, а ваше завдання їх закінчити.- Відстань від центру кола до її будь-якої точки називається .... (Радіус).
- Площа прямокутника обчислюється за формулою .... (S = a * b).
- Фігура, що має три виміри: ширину, довжину і висоту називається .... (Паралелепіпед).
- За формулою * R 2 обчислюється .... (Площа кола).
- Як називається число, наближено дорівнює 3,14 ... (число «пі»).
- Що обчислюють за формулою 2 ** R .... (Довжину окружності).
- Наука, що вивчає властивості фігур називається .... (Геометрія).
- Скільки пройде часу, якщо хвилинна стрілка зробить повне коло? (1 година).
(На магнітній дошці учень складає формули для знаходження площі круга, довжини кола, діаметра через радіус. Учитель в цей час працює з класом.)
Учитель: Хлопці, подивіться уважно на малюнок і дайте відповідь, скільки побудовано кіл?
Як побудувати цю форму?
(Відповіді учнів. Перевіряють формули, складені на магнітній дошці.)
Учитель: А тепер увага на екран! Вибрати правильну відповідь і обґрунтувати його.
1. Радіус зображений відрізком: 1) AB; 2) OD; 3) CD.
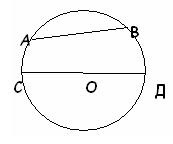
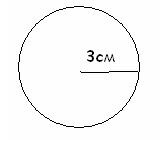
2. Довжина кола з даними радіусом обчислюється:
2) = 2 ** 3 2 = 18 * (см); 3) = 2 ** 6 = 12 * (см).
3. Площа круга 9 * м 2. чому дорівнює радіус: 1) R = 9 м; 2) R = 3 м; 3) R = 4,5 м.
Учитель: Молодці, хлопці. Розминка закінчена. Записуємо в зошитах число і тему уроку.
(На дошці записані завдання.)
Завдання №1. Діаметр окружності підстави Цар-дзвона дорівнює 6,6 м. Знайдіть площу основи Цар-дзвона, число П округлятимете до цілих.
Рішення. R = D: 2, R = 3,3 (м), 3,143, S = * R 2. S = 3 * 3,3 2 = 32,67 (м 2).
Відповідь. площа підстави Цар-дзвона 32,67 м 2.
Завдання №2. У прямокутної пластині просвердлений круглий отвір. Знайдіть площу деталі і її масу, якщо 1 см 2 важить 2 м (число 3).
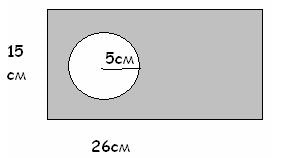
Рішення. Sокружн. = * R 2. Sпрямоуг. = A * b, Sфігури = Sпрямоуг - Sокружн., Sокружн. = 75 см 2. Sпрямоуг = 390 см 2. S = 315 см 2 .m = 315 * 2 = 630 (г).
Відповідь: площа деталі 315 см 2. маса деталі 630 м
Учитель: Хлопці, у вас на столах є роздатковий матеріал. Візьміть кольорові кружечки. Перегибанием знайдіть центр. Відзначте його, проведіть радіус. Обчисліть площу кола (3).
(Хлопці працюють самостійно, потім проводиться перевірка. Рішення записується на дошці.)
Самостійна робота (червоний гурток, R = 2 см; жовтий - 3 см; зелений - 4 см; синій - 5 см).
Учитель: Наступне завдання. Побудувати коло і обчислити її довжину. I - варіант, радіус дорівнює 3 см, II варіант, радіус дорівнює 5 см.
(Хлопці працюють самостійно).
Учитель. Якщо ви вирахували правильно, то при підстановці вашої відповіді в даний вираз вийде вірне рівність. Перевіряємо. (На дошці записана перевірка)
I варіант: + 1,16 = 20
II варіант: + 68, 6 = 100
Учитель: Коло дуже гармонійна фігура. Недарма їй приділялося так багато уваги не тільки вченими, математиками, а й архітекторами, скульпторами, художниками. Подивіться ці репродукції (учитель на свій розсуд може підібрати такі репродукції). Елементи окружності проглядаються в цих шедеврах. Своє застосування окружність знайшла і в народній творчості, зокрема - різьбі по дереву. Орнамент складається з кіл і її елементів. (Рисунок 1), (рисунок 2), (рисунок 3), (рисунок 4).
Учитель: Найпростіша і в той же час найвеличніша з кривих ліній - окружність. Це одна з найдавніших геометричних фігур. Вавилоняни і стародавні індійці вважали найважливішим елементом кола радіус. Слово це латинське і позначає «промінь». Термін радіус вперше зустрічається в книзі «Геометрія» французького вченого Рамуса, виданої в 1569 році, а потім у Франсуа Вієта. Питання про обчислення відношення довжини окружності до діаметру, тобто числа П, займав кращі уми людства протягом тисячоліть. «Пі» - початкова буква грецького слова «perimetron», яке і означає коло. Перші обчислення П на основі строгих теоретичний міркувань було зроблено найбільшим математиком давнини Архімедом, він довів, що. Ідеї Архімеда майже на два тисячоліття випередили свій час. Тільки в XVII столітті вчені змогли продовжити і розвинути праці великого грецького математика. Архімед жив (ок.287-212 р.р. до н.е.) в м Сіракузи на о. Сицилія. Загинув від рук римського воїна. Перед загибеллю Архімед сказав воїну: «Не чіпай мої кола!». Архімеда було 75 років. Скільки б він міг ще зробити відкриттів потрібних людству!
Учитель: Як ви думаєте, чому ж так чудова коло?
(Відповіді дітей) Отже, хлопці, окружності знайшлося широке застосування не тільки в науці, а й у побуті, і в мистецтві.
Учитель: Хлопці, запишіть домашнє завдання. Обчисліть площу пятирублевой монети.