Реологія - наука про процеси деформації і перебігу різних тел в часі. Реологія вивчає механічні властивості систем по прояву деформації під дією зовнішніх напружень. термін
деформація означає відносне зміщення точок системи, при якому не порушується її суцільність. Напруга. що викликає деформацію - відношення сили до площі її застосування. Найпростішими видами деформації є розтягнення і зрушення. Найбільш повну характеристику структурованих систем дає дослідження деформації зсуву, що виникає під дією тангенціальних напружень.
Розрізняють деформації оборотні і залишкові.
Деформації, що зникають після зняття навантаження, називають оборотними. а тіла, можна зупинити відновлюють первісну форму після зняття навантаження, називають пружними тілами.
Деформації, які не зникають після зняття навантаження, називають залишковими. а тіла, які виявляють залишкову деформацію при напружених, що перевищують їх межа пружності, називають пластичними. Одним з видів залишкової деформації є течія, характерне для рідин, при якому величина деформації безперервно збільшується при постійно діючому напрузі.
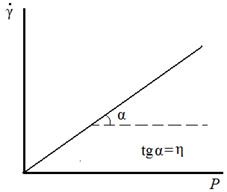
Реологічні властивості ідеально в'язких тіл (ідеальних рідин) підкоряються закону Ньютона і описуються рівнянням:
де Р - напруга зсуву, Па; # 951; - в'язкість рідини, Па · с; - швидкість деформації (зміна деформації в часі) або швидкість течії рідини.
У рівнянні (6.1) роль коефіцієнта пропорційності грає в'язкість (внутрішнє тертя), яка є найважливішим властивістю, що характеризує структуру будь-якої дисперсної системи. В'язкість є реологічні константою досліджуваної рідини, не залежить від способу її вимірювання і визначає здатність рідини чинити опір течією. Величина, зворотна в'язкості. називається плинністю.
Залежність від Р являє собою пряму, що виходить з початку координат. Тангенс кута нахилу цієї прямої до осі абсцис визначає величину в'язкості, а до осі ординат - величину плинності (рис. 6.1).
Для течії ідеальних рідин з капіляра Пуазейль запропонував рівняння, що є окремим випадком рівняння Ньютона:
де # 951; - в'язкість рідини; Р - різниця тисків на кінцях капіляра (тиск течії); # 964; - час витікання рідини з капіляра; К - постійна капіляра (віскозиметра).
За законами Ньютона і Пуазейля в'язкість не повинна залежати від зовнішнього тиску тільки в ламінарному потоці. В умовах турбулентності в'язкість починає збільшуватися зі зростанням тиску і основні закони в'язкої течії виявляються неспроможні.
В'язкість дисперсних систем відрізняється від в'язкості дисперсійного середовища за рахунок заповнення частини розчинника дисперсною фазою. Зі збільшенням концентрації дисперсної фази, в'язкість дисперсної системи збільшується. Зв'язок між в'язкістю дисперсної системи і об'ємною часткою дисперсної фази описується рівнянням Ейнштейна:
де # 951; - в'язкість дисперсної системи; # 951; 0 - в'язкість дисперсійного середовища; # 966; - об'ємна частка дисперсної фази, відношення обсягу частинок дисперсної фази до обсягу дисперсної системи (); # 945; - коефіцієнт, що враховує форму частинок (для частинок сферичної форми # 945; = 2,5).
У міру збільшення концентрації частинок дисперсної фази лінійна залежність # 951; - # 966; порушується в умовах взаємного зіткнення частинок, проте при даній концентрації в'язкість залишається постійною. Подібні системи, що підкоряються рівнянням Ньютона, Пуазейля і Ейнштейна, називають нормальними або ньтоновскімі.
Для структурованих систем спостерігається відхилення від теоретичної залежності вже при малих концентраціях. Такі системи, що не підкоряються рівнянням Ньютона, Пуазейля і Ейнштейна і називають аномальними або неньтоновскімі.
Наявність структури змінює характер перебігу рідини. Для чистих безструктурні рідин спостерігається лінійна залежність між і Р (крива 1. рис. 6.2) з постійним нахилом, відповідному постійної в'язкості.
Для структурованих систем характерні криві зі змінною в'язкістю, що залежить від Р (крива 2. рис. 6.2).
При малих напругах (Р <РТ ) наблюдается медленное течение с малым наклоном. Это течение происходит при максимальной вязкости системы, без разрушения ее структуры, и называется ползучестью .
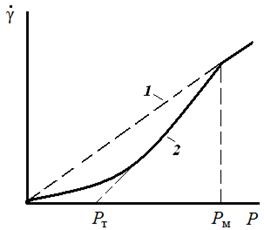
Мал. 6.2. Залежність швидкості деформації від напруги для ньютонівських рідин
Мал. 6.3. Залежність швидкості течії від напруги для неструктурованих (1) і структурованих (2) систем
При збільшенні напруги відбувається зростання швидкості течії, відповідне руйнування структури. В'язкість системи зменшується і відповідає так званої пластичної в'язкості системи (). У цьому випадку крива плинності описується рівнянням Бінгама:
де - межа плинності (мінімальне навантаження, при якій тіло починає текти); - пластична в'язкість, що характеризує здатність структури до руйнування при зміні навантаження.
Величина межі плинності або граничне динамічна напруга зсуву знаходиться екстраполяцією цієї частини кривої до осі абсцис і характеризує зусилля, необхідне для початку руйнування структури. Подальше збільшення напруги викликає повне руйнування структури при Р = РМ. Величина РМ називається граничним напруженням зсуву. Кінцева ділянка кривої течії відповідає закону Ньютона з меншою в'язкістю.
Найбільш загальним рівнянням, що описує протягом неньютоновскіх рідин, є емпіричне рівняння Оствальда - Вейля:
де k і n - емпіричні константи, що відображають властивості матеріалу.
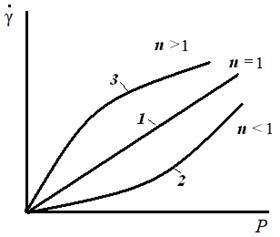
Мал. 6.4. Залежність швидкості течії
від напруги для ньютонівської (1),
псевдопластичних (2) і ділатантні (3) рідин
Відхилення n від одиниці характеризує ступінь відхилення властивостей неньютоновскіх рідин від властивостей ньютонівських рідин. Якщо n = 1, то рідина є ньютонівської і константа k збігається з ньютонівської в'язкістю # 951 ;. при n <1 ньютоновская вязкость уменьшается с увеличением скорости сдвига и напряжения. Соответственно этому жидкости называют псевдопластическими . При n> 1 ньютоновская в'язкість зростає зі збільшенням швидкості зсуву. Відповідно такі рідини називають ділатантні.
Вимірювання в'язкості дисперсних систем, в залежності від швидкості течії, широко використовується на практиці. У технологічному процесі на різних його стадіях в'язкість структурованих дисперсних систем може сильно змінюватися. У ряді випадків, наприклад, при транспортуванні, необхідно, щоб продукт мав максимальну в'язкість, Тобто був структурованим, а для перекачування продукту, навпаки, необхідно створювати таку швидкість течії, яка б відповідала його мінімальної в'язкості.
Питання і завдання для самоконтролю
1. Які структурно-механічні властивості дисперсних систем ви знаєте?
2. Перерахуйте типи структур.
3. Що таке в'язкість? Які види в'язкості ви знаєте? Яким чином кількісно можна розрахувати величину в'язкості?
4. Чим визначається в'язкість дисперсної системи?
глава 7
ОПТИЧНІ ВЛАСТИВОСТІ
ДИСПЕРСНИХ СИСТЕМ
До оптичних властивостей дисперсних систем відносяться: поглинання, віддзеркалення, заломлення, пропускання, розсіювання світла.
Специфіка оптичних властивостей об'єктів колоїдної хімії визначається їх основними ознаками: гетерогенність і дисперсністю. Вивчення оптичних властивостей дисперсних систем є самим оперативним і доступним засобом визначення розмірів частинок, їх форми, структури, а також концентрації. Для колоїдних систем найбільш характерним є поглинання і розсіювання світла.