Завдання 5.
Кожен з двох робочих однаковою кваліфікації може виконати замовлення за 12 годин. Через 4 години після того, як один з них почав виконувати замовлення, до нього приєднався другий робочий, і роботу над замовленням вони довели до кінця вже разом. Скільки годин знадобилося на виконання всього замовлення?
У цьому завданні і не потрібно вводити змінну. Вона буквально виконується по діям.
Давайте простежимо як заповнювалася таблиця.
1) У даному випадку робота для нас абстрактна. Ми не можемо її виміряти в сторінках, деталях, літрах і т.п. У таких випадках позначають роботу за 1 (можна було б і за позначити).
2) Продуктивність обох робочих - частина роботи в годину.
3) Раз перший робочий працював 4 години з продуктивністю, то він виконав частину роботи.
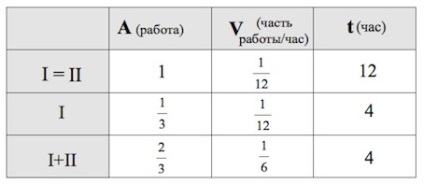
4) Частина роботи -.
5) При спільній роботі продуктивності складаються. Тому удвох робітники працюють зі швидкістю частина роботи в годину.
6) Час роботи знаходимо за формулою. Отримуємо: години.
Нарешті, на виконання всього замовлення потрібно годин.
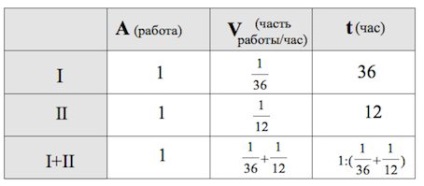
Завдання 6.
Один майстер може виконати замовлення за 36 годин, а інший - за 12 годин. За скільки годин виконають замовлення обидва майстри, працюючи разом?
Завдання 7.
Ігор і Паша фарбують огорожу за 20 годин. Паша і Володя фарбують цей же паркан за 21 годину, а Володя і Ігор - за 28 годин. За скільки годин хлопчики пофарбують паркан, працюючи втрьох?
Як заповнювати перші три рядки таблиці не повинно викликати у вас питання.
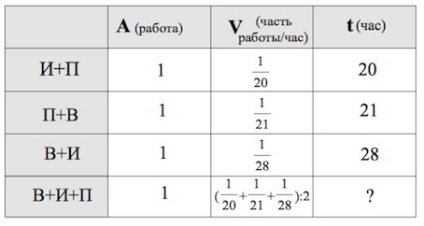
Далі, ми пам'ятаємо, що при спільній роботі продуктивності складаються. Але при додаванні величин з середніх трьох осередків ми отримаємо спільну продуктивність двох Ігорів, двох Павлов і двох Володимирів, якщо так можна висловитися.
Саме тому продуктивність Володимира, Ігоря і Павла дорівнює
Тоді хлопчики пофарбують паркан, працюючи втрьох за годин.
Завдання 8.
Дві труби наповнюють басейн за 7 годин 55 хвилин, а одна перша труба наповнює басейн за 38 годин. За скільки годин наповнює басейн одна друга труба?
Спочатку заповнюємо перший рядок таблиці.
Далі третю, при цьому переводимо хвилини в години.
І, нарешті, ми переходимо до другої рядку. При цьому, оскільки при спільній роботі продуктивності складаються, то продуктивність другої труби є різниця производительностей спільної двох труб і продуктивності першої труби.
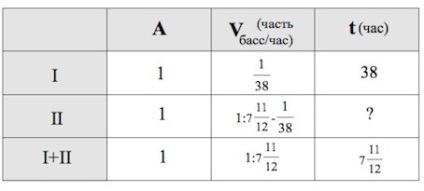
Тоді друга труба заповнить басейн за
Завдання 9.
Петя і Митя виконують однаковий тест. Петя відповідає за годину на 10 питань тексту, а Митя - на 16. Вони одночасно почали відповідати на питання тесту, і Петя закінчив свій тест пізніше Миті на 117 хвилин. Скільки питань містить тест?
Нехай в тесті питань. Швидкість відповідей на питання тесту Петі - 10 питань на годину, Миті - 16 питань на годину.
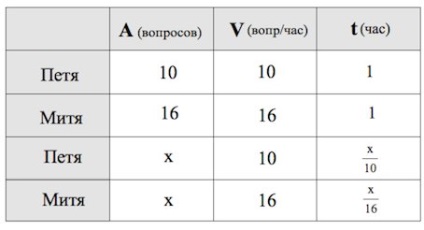
(Час відповіді на весь тест Петром) на 117 хвилин більше (час відповіді на весь тест Митей) згідно з умовою.
Не забуваємо перевести хвилини в години. хвилин годину. Тому
Сайт А. Ларіна ЕгеТренер - О. Себедаш Математика? Легко! ЄДІ? Ок! - І. Фельдман
