Функція ЧПС повертає суму будь-якого ряду регулярних платежів, розрахованих на даний момент при використанні єдиної облікової ставки. Синтаксис функції ЧПС наведено нижче (обов'язкові параметри виділені напівжирним шрифтом).
= ЧПС (ставка; значення1; значення2; ...)
Вхідні потоки представлені у вигляді позитивних значень, а вихідні - у вигляді негативних. Функція ЧПС має ті ж обмеження, що і фінансові функції ПС. ПЛТ. БС. КПЕР і СТАВКА.
Якщо вихідні потоки перевищують входять, функція поверне негативну суму. Точно так же, якщо вхідні потоки перевищують вихідні, функція ЧПС поверне позитивну суму.
Аргумент ставка являє собою ставку дисконту - відсоток, на який майбутні грошові потоки будуть зменшуватися. Фактично це рівень прибутковості, якого прагне домогтися інвестор. Якщо функція ЧПС повертає нуль, це вказує на те, що майбутні грошові потоки забезпечать той рівень прибутковості, який в точності дорівнює заданій процентній ставці.
Якщо значення, що повертається функцією ЧПС. позитивне, значить, майбутні грошові потоки забезпечать більш високий рівень прибутковості, ніж задана процентна ставка. Отримане позитивне значення являє собою ту суму, яку інвестор міг додати в початковий грошовий потік, щоб отримати заданий їм рівень прибутковості.
Якщо ЧПС повертає від'ємне значення, то інвестор не отримує необхідної йому облікової ставки. Ця ставка часто називається порогової рентабельністю. Для досягнення потрібної ставки інвестор повинен зменшити початковий вихідний грошовий потік (або збільшити початковий вхідний потік) на величину, що повертається негативним результатом ЧПС.
Використовувана дисконтна ставка - це єдина ефективна ставка протягом періоду обліку грошових потоків. Таким чином, якщо грошові потоки реєструються щомісяця, то необхідно використовувати щомісячну ефективну ставку.
Визначення функції ЧПС
Функція ЧПС передбачає, що перший платіж виконується в кінці першого періоду.
Це припущення відрізняється від визначення, що використовується більшістю фінансових калькуляторів. Воно також не збігається з визначенням, що використовуються такими установами, як Інститут бухгалтерів США (AIA). Наприклад, останнє визначення встановлює ЧПС як різницю між поточним значенням вхідних і вихідних грошових потоків. Якщо використовувати функцію ЧПС без додаткової корекції, то результат не буде відповідати визначенню AIA.
Основне призначення функції ЧПС - з'ясувати, чи забезпечать інвестиції очікуваний рівень прибутковості. Типова послідовність грошових потоків складається з початкового вихідного потоку, за яким слідує серія вхідних потоків. Наприклад, ви купуєте візок для приготування хот-догів і напівфабрикати (початковий вихідний потік) і влітку щодня продаєте їх на вулиці (серія вхідних потоків). Якщо в якості аргументу використовувати початковий вихідний потік, функція ЧПС передбачає, що початкові інвестиції виконуються не зараз, а в кінці першого місяця (або через який-небудь інший часовий період).
На малюнку показаний робочий лист з обчисленням чистої приведеної вартості для ряду грошових потоків: початкового вихідного потоку об'ємом в 20 тисяч доларів, ряду місячних вхідних потоків і 8% -ного дисконту.
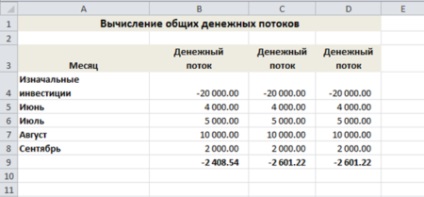
Формули в рядку 9 наступні:
В9: = ЧПС (0.08; В4: В8)
С9: = ЧПС (0.08; С5: С8) + С4
D9: = ЧПС (0.08; D4: D8) * (1 + 0.08)
Формула в комірці В9 дає результат, що відрізняється від інших двох. Вона передбачає, що інвестиція в 20 тисяч доларів зроблена протягом першого місяця. Існують додатки, в яких використовується саме такий порядок розрахунків, проте в них рідко (якщо взагалі) використовуються початкові інвестиції. Решта дві формули відповідають на питання, чи будуть інвестиції, що вносяться негайно, давати приріст 8%. Формули в осередках С9 і D9 дають однаковий результат і є взаємозамінними.
Приклади використання функції ЧПС
У цьому розділі міститься кілька прикладів, які демонструють використання функції ЧПС.
Багато обчислення чистої приведеної вартості починаються з початкового вихідного грошового потоку, за чим слід серія вхідних потоків. У представленому далі прикладі в момент часу 0 був куплений снігоочисник. Протягом наступних десяти років цей снігоочисник використовувався для прибирання доріг, що дозволяло отримувати дохід. Практика показує, що такого роду снігоочисник може працювати десять років, після чого його ремонт вже не має сенсу. На малюнку показаний робочий лист з обчисленнями чистої приведеної вартості майбутніх грошових потоків, асоційованих з покупкою снігоочисника.
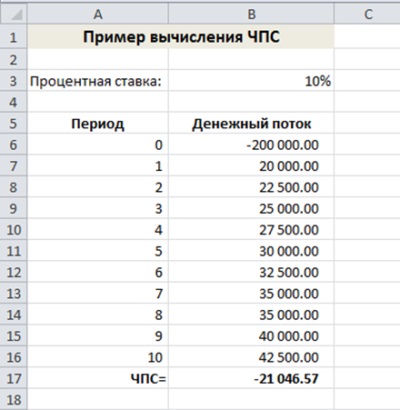
Функція ЧПС в осередку В17 використовує наступну формулу, яка повертає суму - 21046,57 доларів:
Чиста приведена вартість в даному прикладі виявилася негативною. Це свідчить про те, що покупку снігоочисника не можна назвати вдалою інвестицією. На результат вплинуло кілька факторів.
• По-перше, "вдалою інвестицією" можна назвати ту, яка приносить, як мінімум, 10% прибутку. Якщо вас задовольняє менша віддача від вкладених коштів, підставте її в формулу.
• Майбутні грошові потоки часто можна оцінити, але не завжди. В даному випадку потенційний покупець снігоочисника передбачає зростання доходів протягом 10 років. Якщо у покупця є десятирічний контракт на прибирання снігу, він може точно оцінити майбутні входять грошові потоки. В іншому випадку оцінити майбутні доходи можна, тільки грунтуючись на власному досвіді і прогнозах.
• На закінчення, якщо вам вдасться домовитися з продавцем снігоочисника про знижку, десятирічна інвестиція може виявитися цілком розумною.
Відсутність початкової інвестиції
На приклад покупки снігоочисника можна подивитися і з іншої точки зору. У попередньому прикладі вартість снігоочисника була представлена в якості початкової інвестиції. У цьому прикладі потрібно дізнатися, чи зможе покупка снігоочисника принести десятипроцентну прибуток. Функцію ЧПС можна також використовувати і для обчислення величини початкової інвестиції, здатної забезпечити необхідну прибуток. Що стосується даному наприклад, це означає визначити, скільки має сенс віддати за снігоочисник. На малюнку показано обчислення приведеної вартості серії грошових потоків в припущенні відсутності початкової інвестиції.
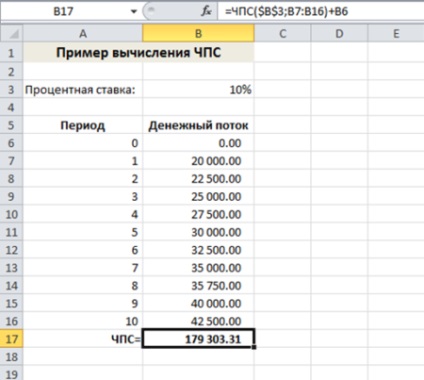
Для обчислення чистої приведеної вартості в осередку В17 використовується наступна формула:
Отже, якби майбутній власник снігоочисника зміг би його купити за 179 303 долара, йому можна було б розраховувати на 10% -ву віддачу від інвестицій (в припущенні, що розрахунки доходів точні). Вміст комірки В6 додається в формулу виключно з міркувань однаковості з попереднім прикладом (так як початкові інвестиції дорівнюють нулю).
Початковий вхідний потік
На малюнку показаний приклад, в якому початковий грошовий потік є вхідним. Подібно до попереднього прикладу, результатом формули буде сума початкових інвестицій, які необхідні для отримання потрібної ставки прибутковості. Однак в цьому випадку передбачається, що входять інвестиції будуть отримані негайно.
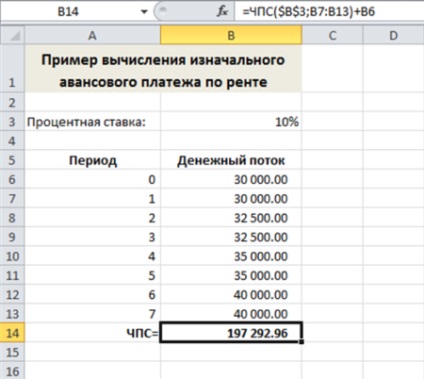
Обчислення чистої приведеної вартості в осередку В14 виконуються за такою формулою:
Цей приклад може здатися незвичайним, проте в реальному житті така ситуація часто трапляється в сфері нерухомості, коли рента виплачується авансом. Як випливає з формули, ви можете виплатити по ренті 197292,96 доларів, і ця сума погасить майбутні виплати. Рента за перший рік виплачується авансом, тому вона вказана в нульовому періоді.
В останньому наведеному прикладі відсутня одна ключовою елемент: перехід власності після закінчення семи років. Ви можете орендувати житло вічно, в разі чого буде потрібно постійно збільшувати в розрахунках кількість часових періодів. Можете також продати нерухомість.
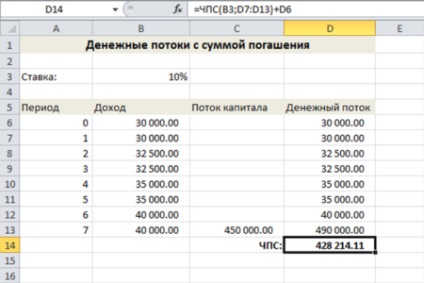
Чиста приведена вартість в осередку D14 обчислюється за такою формулою:
В даному прикладі передбачається, що інвестор виплачує за нерухомість поступово 428214,11 доларів, а потім продає нерухомість за 450 тисяч доларів, що приносить йому 10 відсотків прибутку.
Величина початкової інвестиції і суми погашення
У цьому прикладі використовуються ті ж грошові потоки, що і в попередньому, за винятком того, що власник об'єкта нерухомості знає, скільки хоче отримати. Це типовий приклад інвестицій, коли мета полягає в тому, щоб з'ясувати, чи перевищує запитувана ціна бажану ставку, і якщо так, то на скільки.
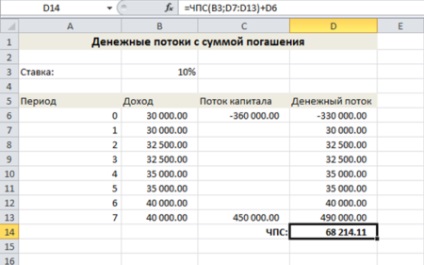
Наступна формула показує, що при запитуваною ціною 360 тисяч доларів дисконтовані вхідні потоки забезпечать прибуток в 68214,11 доларів:
Позитивне значення чистої приведеної вартості показує, що інвестор може заплатити запитувану суму і забезпечити собі потрібну прибутковість. Отриманий результат також показує, що інвестор може заплатити на 68214,11 доларів більше запитуваної ціни і все одно добитися потрібної йому прибутковості.
Майбутні вихідні потоки
Звичайна схема інвестицій передбачає наявність початкового вихідного грошового потоку, компенсується періодичними вхідними потоками, але на практиці це не завжди так. Гнучкість функції ЧПС полягає в тому, що вона дозволяє поєднувати в аналізованому періоді позитивні і негативні значення.
У наступному прикладі передбачається, що компанія планує випускати новий товар, і для цього потрібно інвестувати в покупку устаткування 475 тис доларів, а після закінчення п'яти років витратити на його капітальний ремонт ще 225 тисяч доларів. Також передбачається, що новий товар не буде прибутковим на початку, але поступово його прибутковість буде збільшуватися.
На малюнку показаний робочий лист, що описує ці грошові потоки.
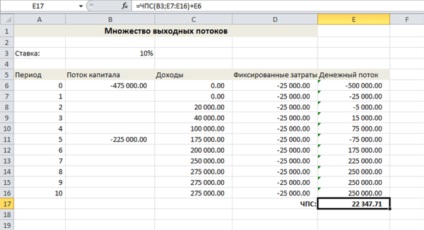
Позитивне значення чистої приведеної вартості означає, що для компанії є сенс інвестувати в обладнання та почати випуск нового товару. Якщо вона це зробить і оцінка зростання популярності товару виявиться точною, компанія отримає прибуток понад 10% від суми інвестицій.
Невідповідні періоди процентної ставки
У попередніх прикладах передбачалося, що процентна ставка нараховується за ті ж періоди, за які здійснюється оборот грошових потоків. У той же час на практиці часто ці періоди не відповідають один одному. Найчастіше задається річна процентна ставка бажаної прибутковості, а грошові потоки мають місячну або квартальну періодичність. В цьому випадку процентну ставку потрібно привести до відповідної періодичності.
На малюнку нижче показані розрахунки з щоквартальними авансовими виплатами 12 тисяч доларів. Також показана початкова ціна (700 тисяч доларів) і ціна продажу (900000 доларів). Зверніть увагу на те, що, оскільки рента проводиться авансовими платежами, ціна змінюється. Однак по закінченню трьох років (12 кварталів) застосовується той же правило, і рента виплачується новим власником. Якщо ефективність інвестиції в 1% вам здається достатньою, чиста приведена вартість складе 166099,72 доларів.
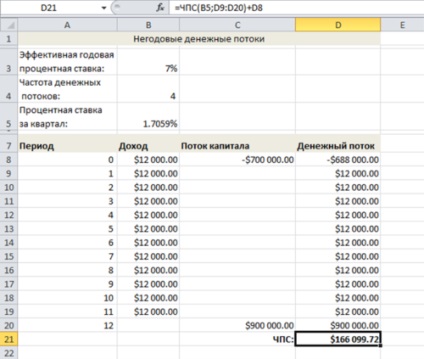
У деяких ситуаціях визначення частоти грошових потоків є простою операцією. Наприклад, в договорі оренди чітко вказана частота виплати ренти. Коли майбутні грошові потоки від використання купленого товару нескладно передбачити, використовуються наближені оцінки. В цьому випадку визначити, який період використовувати краще (місячний, квартальний або річний), не так просто. У загальному випадку частота повинна відповідати точності даних. Це означає, що якщо обсяг продажів оцінюється на рівні року, не варто ділити це число на 12, щоб отримати оцінку місячного обсягу продажів.
На малюнку нижче продемонстровано відмінність застосовуваних підходів. У ньому використані ті ж дані, що і на малюнку вище, проте передбачається, що річна рента в 48000 доларів виплачується в кінці року. При тих же розрахункових 7% річних ЧПС складе вже 160635,26 доларів.
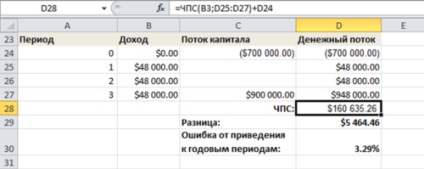
Використання функції ЧПС для обчислення накопичувальних величин
У цьому розділі вашій увазі представлено два приклади використання функції ЧПС для обчислення майбутніх значень і накопичень. Приклади засновані на наступному співвідношенні:
Обчислення майбутнього значення
Дані цього прикладу можна побачити на малюнку нижче. Обчислення чистої приведеної вартості виконується в осередку В15 за такою формулою:
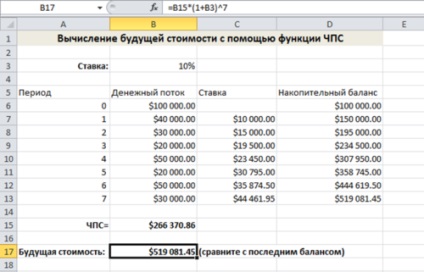
В осередку В17 майбутня вартість обчислюється за такою формулою:
У стовпці D формула обчислює поточний баланс процентної ставки. Вона обчислюється шляхом множення процентної ставки на значення балансу в попередньому місяці. Поточний баланс являє собою суму попереднього балансу, ставки і грошових потоків поточного місяця.
Дуже важливо правильно встановити знаки грошових потоків. Якщо поточний баланс в попередньому місяці був негативним, то і ставка буде негативною. Правильне визначення знаків потоків і застосування підсумовування переважніше використання знаків в формулах для ставки і балансу.
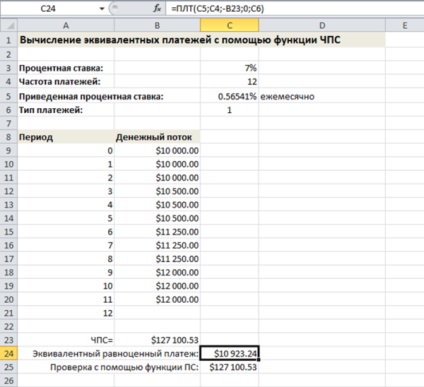
Згладжування сум платежів
Функція ПЛТ використовується для обчислення платежів, еквівалентних заданої чистої приведеної вартості. Можна також використовувати функцію ЧПС. вкладену в функцію ПЛТ. для обчислення одноразового платежу, еквівалентного серії змінюються платежів.
Це завдання досить типова: іноді потрібно обчислити зважений за часом один платіж, який замінює собою серію послідовних платежів. Як приклад може виступати платіж, який замінює собою ряд послідовних, збільшуються за сумою платежів. У прикладі, показаному на малюнку, формула в комірці С24 повертає значення 10923,24 доларів. Це рівноцінні платежі, здатні замінити собою послідовність платежів в стовпці В.