Знання учнів, як правило, знаходяться в прямій залежності від обсягу і систематичності, і самостійної діяльності. У зв'язку з цим А. Дістервег (1790-1866, ньому. Педагог-демократ, послідовник Песталоцці) писав, що «розвиток і освіта жодній людині не можуть бути дані і повідомлені. Всякий, хто бажає до них прилучитися, повинен досягти цього власною діяльністю, власними силами, власною напругою. Ззовні він може отримати тільки збудження ».
Для того щоб знання учнів були результатом їх власних пошуків, необхідно організувати ці пошуки, управляти учнями, розвивати їх пізнавальну діяльність.
- алгебраїчне
- топологічний
- порядкове
- проективне
- метричний
Кожен учень здатний мислити, розуміти, міркувати згідно домінуючого у нього кластера мислення.
Наше завдання розвинути математичне мислення за різними напрямками. У цьому допомагає рефлексивна робота в групах. Спільна діяльність призводить до вірного рішення, міцному засвоєнню матеріалу - і, найголовніше, відбувається осмислення і розуміння розв'язуваної задачі.
Китайська мудрість говорить «Я чую - я забуваю, я бачу - я запам'ятовую, я роблю - я засвоюю»
Тема уроку: «Конус» (2 ч. 11 клас)
Мета уроку:- Ввести поняття конічної поверхні, конуса, елементів конуса (бокова поверхня, основа, вершина, що утворює, вісь, висота), поняття усіченого конуса;
- Вивести формули для обчислення площ бічної і повної поверхонь конуса і усіченого конуса;
- Вчити учнів вирішувати завдання по цій темі.
- Сприяти творчому сприйняттю учнями навчального матеріалу і їх бажання самовдосконалюватися.
- Виховувати організованість, дисциплінованість, відповідальність за свою працю і працю однокласників.
Тип уроку: вивчення нового матеріалу.
Обладнання уроку: інтерактивна дошка, таблиці, моделі конусів, матеріал для виготовлення моделей: спиці, модель площині (пінопласт), папір, клей, ножиці, циркуль, транспортир, лінійка.
Форма організації діяльності учнів. г рупповая.
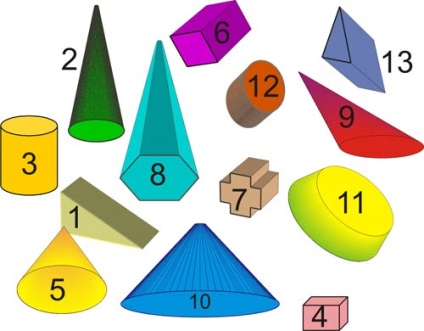
1. Фронтальна робота- Із запропонованих геометричних фігур вибрати конус
- Знайомство з конічною поверхнею
Визначення №1 Конічна поверхня називається поверхня, утворена рухом прямої, яка проходить через дану точку і перетинає дану плоску лінію.
Пряма а - утворює;
Плоска лінія MN - напрямна.
Незамкнута конічна поверхня
Якщо напрямна - замкнута, то конічна поверхня - замкнута.
Визначення №2Конусом називається тіло, обмежене замкнутою конічною поверхнею і перетинає її площиною.
Знайомство з конусом і його елементами
SO - висота конуса
S - вершина конуса
Крива ABA - напрямна.
Б) Нехай прямокутний прямокутник SOA обертається навколо катета SO; при повному обороті гіпотенуза AS описує конічну поверхню, катет OA описує коло.
Таке тіло називається конусом обертання. (Прямий круговий конус).
Прямий круговий конус
S - вершина конуса
SO = h - висота конуса
Підстава конуса - коло (О; r)
Про - центр підстави,
AO = OB = r - радіус підстави кола
D SAB - осьовий переріз
a || b, b SO, a SO
Поняття бічний (повної) поверхні.
II. Робота в групах (3-5 чоловік)
(Завдання лунає кожній групі на картці)
Завдання по темі «Конус»
1) Зобразіть конус. За малюнком визначте всі елементи конуса.
2) За заданою моделі конуса побудуйте розгортку цього конуса. Визначте відповідність елементів розгортки конуса, креслення і моделі конуса.
3) З листа щільного паперу виготовити конус, щоб його повна поверхня: S 110 см2 при радіусі підстави r 3.1 см.
Визначте які інструменти вам для цього знадобляться, які розрахунки необхідні зробити, які формули доведеться згадати, а які вивести нові?
4) Оформіть роботу на місці за планом:
А) Які у вас розподілилися обов'язки в групі в процесі виконання завдань:- генератор ідей;
- конструктор;
- розраховувач;
- оформлювач;
- виробник.
- Необхідні розрахунки для виготовлення моделі конуса. (Креслення. Формули. Висновок)
- Виготовлення конуса.
5) Модель конуса готова.
6) Складіть формулу для розрахунку площі перетину, паралельного основи конуса і ділить висоту конуса у відношенні 1: 3, рахуючи від вершини
7) Складіть формулу для розрахунку площі перетину, що проходить через вісь конуса. Чому дорівнює кут при вершині даного перетину?
8) Яким чином можна з вашої моделі отримати усічений конус? Розрахувати його повну поверхню використовуючи завдання (6).
9) Складіть і вирішите ще три завдання на дану тему.
Зауваження: учитель виступає в ролі консультанта при вирішенні завдань, користуючись вопросамі- підказками і спираючись на ключові слова.
Однією з груп було дано більш легкі завдання:
№1. Заповнити пропуски:- Пряма, яка при русі утворює конічну поверхню, називається ...;
- Лінія, яку перетинає утворює, називається ... ..;
- Конус обертання - окремий випадок ..., коли підстава конуса -. а основа висоти -. ;
- Перетин конуса обертання площиною, паралельної підставі, - .... Знайдіть площу перерізу.
- Якщо осьовий переріз конуса- рівносторонній трикутник, то конус ... ..Сделать креслення:
№2. Вирішіть задачу, заповнюючи пропуски.
В розгортці бічній поверхні конуса центральний кут дорівнює 200 o. Знайти кут між твірною і підставою конуса.
Дано: ВSB = 200 o. SA = L, ОВ = r