Рішення щодо розвитку складської мережі необхідно приймати на основі аналізу повної вартості, що означає облік всіх економічних змін, що виникають при зміні кількості складів в логістичній системі.
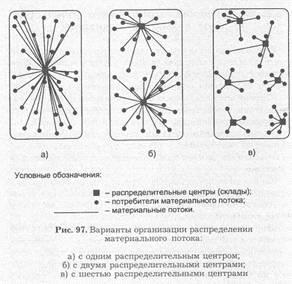
Розглянемо модель системи розподілу матеріального потоку, представлену на рис. 97. Припустимо, що підприємство-постачальник, обслуговує мережу оптових покупців, розташованих на певній території. Кількість покупців і обсяги споживаних ними потоків в рамках даного завдання є величинами постійними.
На малюнку представлено три варіанти організації розподілу: за допомогою одного, двох або шести складів (відповідно малюнки а, б і в). Очевидно, що в разі прийняття варіанту (а) транспортні витрати з доставки будуть найбільшими. Варіант (в) припускає наявність шести розподільних центрів, максимально наближених до місць зосередження споживачів матеріального потоку. В цьому випадку транспортні витрати по товароснабженію будуть мінімальними. Однак поява в системі розподілу п'яти додаткових складів збільшує експлуатаційні витрати, витрати на доставку товарів на склади, витрати на управління всією розподільної системою. Не виключено, що додаткові витрати в цьому випадку можуть значно перевищити економічний виграш, отриманий від скорочення пробігу транспорту, що доставляє товари споживачам. Тому, можливо, що краще виявиться варіант (б), згідно з яким район обслуговується двома складами.
Як бачимо, при зміні кількості складів у системі розподілу частина витрат, пов'язаних з процесом
доведення матеріального потоку до споживача, зростає, а частина знижується. Це дозволяє ставити і вирішувати завдання пошуку оптимальної кількості складів. Розглянемо графічний метод розв'язання даної задачі.
Виберемо в якості незалежної змінної величину N - кількість складів, через які здійснюється постачання споживачів. В якості залежних змінних будемо розглядати наступні види витрат:
♦ транспортні витрати;
♦ витрати, пов'язані з експлуатацією складського господарства;
♦ витрати, пов'язані з управлінням складською системою;
♦ втрати продажів, викликані видаленням постачає складу від споживача.
Для визначення оптимальної кількості складів необхідно в розрізі всієї системи розподілу оцінити, як в залежності від зміни N змінюються ті чи інші витрати і втрати.
Охарактеризуємо залежність витрат кожного виду від кількості складів.
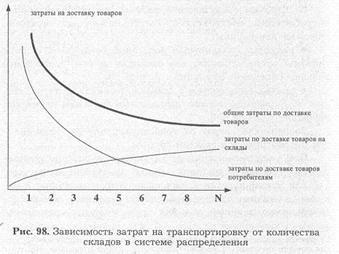
1. Залежність величини витрат на транспортування від кількості складів у системі розподілу (функція f1. Рис. 98).
Весь обсяг транспортної роботи з доставки товарів споживачам, відповідно і транспортних витрат, ділять на дві групи:
♦ витрати, пов'язані з доставкою товарів на склади системи розподілу, тобто витрати на так звані далекі перевезення (функція f1 ', рис. 98),
♦ витрати з доставки товарів зі складів споживачам, т. Е. Витрати на так звані ближні перевезення (функція f1 ", рис. 98).
Залежність витрат на транспортування від числа складів розглянемо для кожної групи.
При збільшенні кількості складів у системі розподілу вартість доставки товарів на склади зростає, оскільки збільшується кількість поїздок, а також сукупна величина пробігу транспорту. Характер залежності не прямолінійний, так як тут є умовно-постійна та умовно змінна складові, в результаті чого витрати з доставки зростають повільніше, ніж відстань.
Інша частина транспортних витрат - вартість доставки товарів зі складів споживачам, зі збільшенням кількості складів знижується. Це відбувається в результаті різкого скорочення пробігу транспорту.
Сумарні транспортні витрати (функція f1. Рис. 98) при збільшенні кількості складів у системі розподілу, як правило, зменшуються.
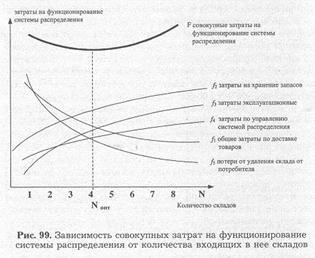
Збільшення кількості складів у системі розподілу тягне за собою скорочення зони обслуговування окремого складу, а, отже, і розміру запасу на окремому складі. Однак запас на окремому складі скорочується не настільки швидко, як зона обслуговування, в результаті сумарний запас в розподільчій системі зростає.
Перша причина - необхідність утримання страхового запасу. У моделі з декількома складами страховий запас, в загальному випадку, необхідно створювати на кожному складі. Скорочення складської мережі тягне за собою концентрацію страхового запасу і загальне зниження потреби в ньому. Очікувану економію розраховують за допомогою закону квадратного кореня, згідно з яким розмір страхового запасу, а, отже, і сума витрат на його утримання, зростає пропорційно кореню квадратному з числа складів.
Інша причина зростання сумарного запасу полягає в тому, що потреба складів в деяких групах товарів при зменшенні зони обслуговування може виявитися нижче мінімальних норм, за якими товар отримують самі склади. Це змусить завозити дану групу на склади в кількості, що перевищує потребу, що також спричинить за собою зростання розміру запасу. Можна навести й інші причини того, що при збільшенні кількості складів сукупний розмір запасу в системі розподілу збільшується.
3. Залежність витрат; пов'язаних з експлуатацією складського господарства від кількості складів у системі розподілу (функція f3. рис. 99).
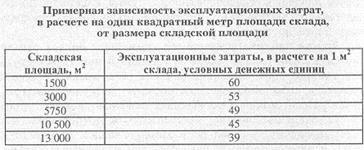
Орієнтовна залежність величини питомих експлуатаційних витрат від розміру складу (сфера торгівлі товарами народного споживання) наведена в табл. 18.
4. Залежність витрат, пов'язаних з управлінням розподільної системою від кількості вхідних в неї складів (функція f4. Рис. 99).
Характер цієї залежності представлений кривої f4. Тут також діє ефект масштабу, в зв'язку з чим при збільшенні кількості складів крива витрат на системи управління робиться більш пологої.
Обов'язковою умовою можливості ефективного функціонування розподільної системи, що має кілька складів, є комп'ютеризація управління.
При відсутності коштів обчислювальної техніки крива витрат на управління може прийняти зовсім інший вид, тобто збільшення кількості складів спричинить за собою різке збільшення витрат на систему управління складським господарством. Слід зазначити, що розвиток розподільних складських систем в середині справжнього століття стримувалося саме відсутністю коштів автоматизованої обробки інформаційних потоків.
5. Залежність втрат продажів, викликаних скороченням числа складів і відповідним видаленням постачає складу від споживача, від кількості складів системи розподілу (функція f5. Рис. 99).
При скороченні кількості складів середня відстань до обслуговуваних пунктів зростає. Стає складніше підтримувати сервіс на колишньому рівні. Складніше поставляти вантажі по системі "точно в строк", так як зрослі витрати на траспортування збільшують економічно оптимальний розмір партії, що відвантажується.
Залежність сукупних витрат на функціонування системи розподілу від кількості вхідних в неї складів (функція F) отримують шляхом додавання всіх, наведених на рис. 99 графіків. Абсциса мінімуму кривої сукупних витрат дасть оптимальне значення кількості складів у системі розподілу (у нашому випадку - 4 склади).
Припустимо, що згадане підприємство-постачальник має на території обслуговування шість складів. Перехід до системи обслуговування за допомогою чотирьох складів супроводжується збільшенням одних витрат і
На завершення слід зазначити, що в останні роки в країнах західної Європи спостерігається тенденція скорочення кількості складів, особливо в роздрібній торгівлі. При цьому, незважаючи на зростання транспортних витрат, в цілому по системі розподілу спостерігається економія коштів, особливо за рахунок скорочення страхових запасів.