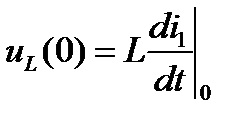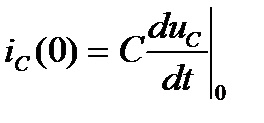Постійні інтегрування, що входять до виразу для вільних складових, обчислюють, підставляючи відомі початкові умови в вирази для шуканої функції і її (n - 1) похідних для моменту часу t = 0 + (n - кількість коренів характеристичного рівняння).
У найзагальнішому випадку, коли характеристичне рівняння має
n коренів і рішення для перехідного струму або напруги записується у вигляді
. для знаходження постійних інтегрування А1. А2, ...... А n потрібно скласти систему n рівнянь такого вигляду
У цих рівняннях - значення вимушених складових для
t = 0 +.
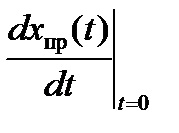
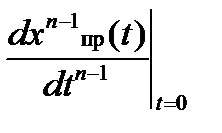
Якщо в задачі розглядається перехідний процес в ланцюзі постійного струму, то. а всі похідні дорівнюють нулю.
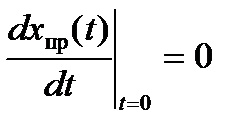
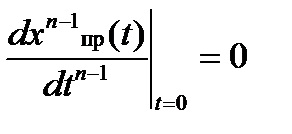
У ланцюзі синусоїдального струму примушені складові змінюються теж за синусоїдальним законом. перша похідна для них визначається виразом.
Для моменту часу t = 0.
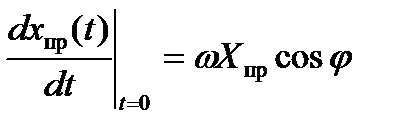
У таблиці 2.6 наведені вирази для перехідних струмів або напруг і їх перших похідних для випадку перехідного процесу в ланцюзі постійного струму.
Рівняння для розрахунку постійних інтегрування наведені в останньому стовпчику таблиці, вони виходять, якщо в вирази перехідної величини і першої похідної підставити t = 0.
Таблиця 2.6 - Рівняння для розрахунку постійних інтегрування
Вирази для перехідних струмів і напруг
Необ-хідні началь-ні умови
Вирази перших похідних для перехідних струмів і напруг, що використовуються для розрахунку постійних інтегрування
Рівняння для розрахунку постійних інтегрування (при перехідному процесі в цепіпостоянного струму)
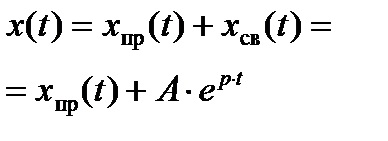
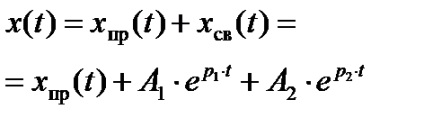
;
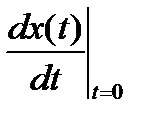
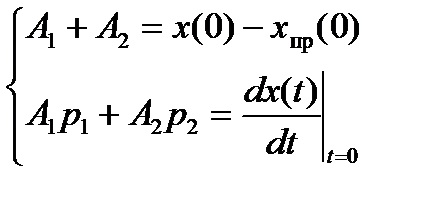
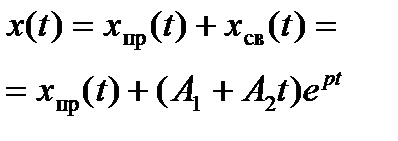
;
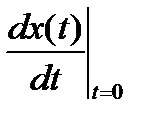
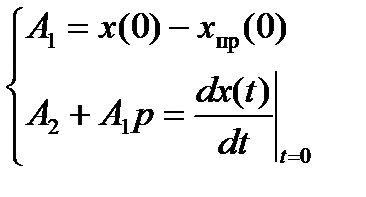
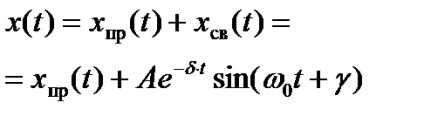
;
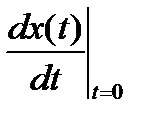
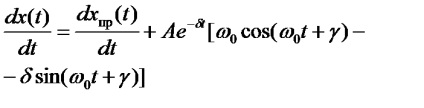
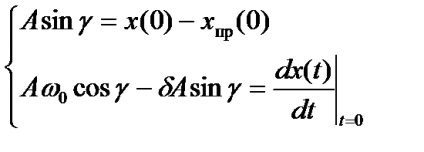
Для визначення постійних інтегрування за формулами таблиці 2.6 необхідно попередньо розрахувати початкові умови.
Початковими умовами називаються значення струмів, напруг і їх похідних в початковий момент перехідного процесу, при.
Початкові умови діляться на незалежні і залежні.
Незалежні початкові умови - це значення струмів індуктивних елементів і напруг ємнісних елементів для часу
Незалежні початкові умови визначаються із законів комутації. ; .
Вони можуть бути нульовими і ненульовими.
Зовсім початкові умови - це значення всіх інших струмів, напруг і похідних за часом струмів і напруг для часу. Зовсім початкові умови визначаються:
- після того, як розраховані незалежні початкові умови;
- з рівнянь за законами Кірхгофа для послекоммутаціонной схеми, записаних для часу.
Кількість початкових умов, які потрібно розрахувати дорівнює кількості постійних інтегрування у виразі перехідною величини. Як випливає з таблиці 2.6, якщо характеристичне рівняння має один корінь і в вираз вільного струму або напруги входить одна невідома постійна інтегрування, для її визначення необхідно попередньо розрахувати тільки одне початкова умова: значення самої функції. Якщо невідомих постійних інтегрування - дві, то для їх визначення попередньо розраховують два початкових умови: значення самої функції і її першої похідної
Е = 100 В, R1 = 10 Ом, R2 = 10 Ом,
R3 = 10 Ом. L = 0,1 Гн
Спочатку знайдемо незалежне початкова умова. для даної схеми - це
струм . так як це струм через індуктивність. За першим законом комутації він буде дорівнює струму через цю ж індуктивність в останній момент перед комутацією.
До комутації в ланцюзі (рисунок 2.36) протікав один постійний струм
Цей струм постійний і від часу
не залежить, тому для часу
За першим законом комутації
Решта шукані початкові значення струмів струми і напруги на індуктивності є залежними початковими умовами.
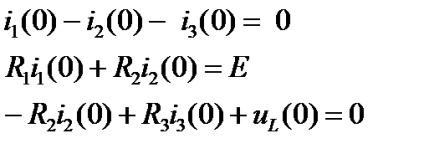
Невідомими в цих рівняннях є. Їх можна знайти, вирішивши складену систему рівнянь будь-яким методом в Mathcad або вручну, наприклад, за допомогою підстановки.
З першого рівняння висловимо і підставимо його в друге рівняння, отримаємо.
Приклад 2 (рисунок 2.37)
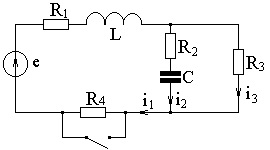
Е = 100 В; = 10 Ом;
= 20 Ом; L = 0,05 Гн; С = 250 мкФ.
Зі схеми до комутації знайдемо незалежні початкові умови (струм індуктивного і напруга ємнісного елементів для моменту часу t = 0). Оскільки в галузі з ємнісним елементом при Е = const струм відсутній, то: i1 (0) = i3 (0-) = E / (R1 + R3 + R4) або i1 (0) = 100 / (10 + 10 + 20) = 2,5 A,
Для визначення залежних початкових умов записуємо рівняння за законами Кірхгофа для схеми після комутації для моменту часу t = 0 +:
.
Підставляючи в ці рівняння знайдені вище незалежні початкові умови i1 (0) і uC (0), знаходимо: A; A; B.
Похідна струму через індуктивність знаходиться з формули