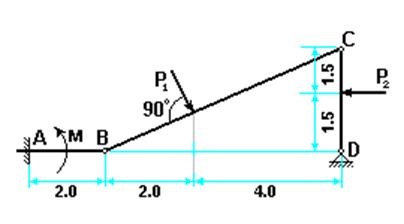
На конструкцію, що складається зі стрижнів АВ, ВС і CD діють зовнішні зосереджені навантаження Р1 і Р2. На ланка АВ діє пара сил з моментом М. З'єднання в точках В і С - шарнірні. У точці А кріплення ланки АВ - жорстка плоска закладення. У точці D кріплення ланки CD - шарнір. Визначити реакції в точках А і D, а також зусилля в шарнірах В і С. Розміри показані на малюнках в метрах, значення сил: Р1 = 4 кН, Р2 = 3 кН, момент пари М = 6 кН × м. Вагою елементів конструкції знехтувати.
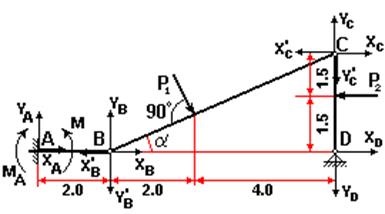
Розглянемо рівновагу ланок складовою конструкції AB, BC і CD, вважаючи внутрішні реакції в шарнірах C і D зовнішніми для відповідних ланок: реакції X'B. Y'B діють на ланку AB з боку ланки BC, реакції XB. YB діють на ланку BC з боку ланки AB, реакції X'C. Y'C діють на ланку BC з боку ланки CD, реакції XC. YC діють на ланку CD з боку ланки BC.
Для подальших обчислень нам будуть потрібні тригонометричні функції кута a:
Для кожної ланки запишемо рівняння рівноваги у вигляді рівнянь для плоскої системи сил:
Маємо дев'ять алгебраїчних рівнянь для визначення дев'яти невідомих: XA. YA. MA. XB = X'B. YB = Y'B. XC = X'C. YC = Y'C. XD. YD. Підставляючи в ці рівняння рівноваги чисельні значення з умов завдання і значення тригонометричних функцій для кута a знайдемо шукані реакції:
Знаки показують, що реакції XA. XB. YC. YD спрямовані протилежно показаному на малюнку.