1. При поступальному русі ланки рівнодіюча сил інерції всіх елементарних мас
прикладена в центрі S мас ланки і спрямована протилежно прискоренню центру S мас ланки (рис. 12).
2. Якщо ланка здійснює обертальний рух навколо осі, що збігається з центром мас, то сили інерції всіх елементарних мас можна звести до пари сил з моментом (рис. 13):
де - статичний момент інерції ланки щодо осі, що проходить через центр мас перпендикулярно площині руху.
Знак «-» у формулі для Мін вказує на те, що момент спрямований в бік, протилежний кутовому прискоренню.
Моментом інерції тіла Js щодо будь-якої осі називається величина, що дорівнює сумі творів елементарних мас цього тіла на квадрат їх відстані до цієї осі:
3. Ланка здійснює складний рух (рис. 14). У цьому випадку рух ланки розкладається на переносне поступальний зі швидкістю і прискоренням центру мас і на відносне обертальний рух навколо центру мас.
Сили інерції всіх елементарних мас зводяться до рівнодіючої силі інерції і до пари сил з моментом. .
Сила інерції прикладена в центрі S мас ланки і спрямована в бік, протилежний прискоренню центру мас; момент інерції спрямований у бік, протилежний # 949; .
4. Ланка здійснює обертальний рух щодо осі, що не проходить через центр мас ланки (рис. 15).
Цей випадок розглядаємо як загальний випадок складного руху ланки: сили інерції всіх елементарних мас також зводяться до рівнодіючої силі інерції і до пари сил з моментом.
1.5.2 Визначення Fін і Mин для кривошипно-ползунного механізму (рис. 16)
Нехай центр мас 1 ланки S1 знаходиться в точці А (в центрі обертання ланки 1), S3 збігається з точкою С; S2 - посередині ланки 2.
Для визначення Fінi і Mінi; треба знати лінійні прискорення центрів мас і кутові прискорення ланок, для чого (при графічному вирішенні завдання) необхідно побудувати плани швидкостей і прискорень (рис. 17, а, б).
Ланка 1 здійснює рівномірний обертальний рух (так як # 969; 1 = const. то). Центр мас нерухомий і as = 0, отже, Fін1 = 0.
Ланка 2 здійснює плоскопараллельное рух:
. .
Для знаходження прискорення точки S2 скористаємося теоре-мій про подібність:
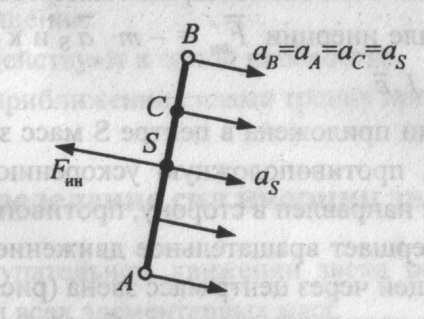
Мал. 12. Сила інерції ланки при його поступальному русі (момент сил інерції дорівнює нулю)
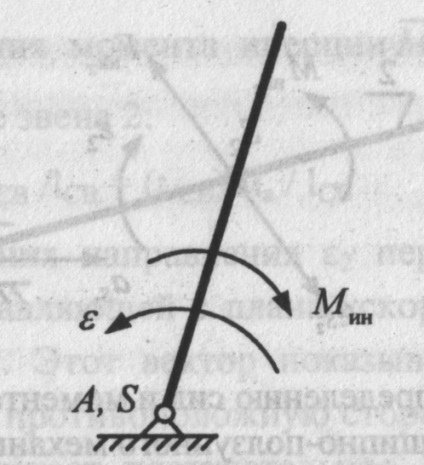
Мал. 13. Момент інерції ланки при його обертанні навколо осі, що проходить через центр мас ланки (сила інерції дорівнює нулю)
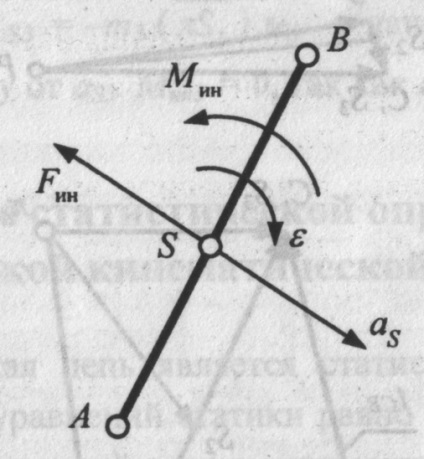
Мал. 14. Сила і момент сил інерції ланки, що здійснює складний рух
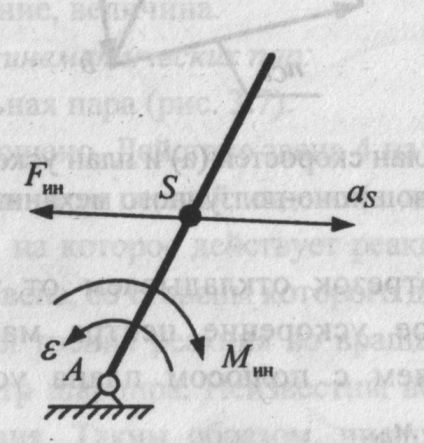
Мал. 15. Сила інерції і момент сил інерції ланки, що обертається навколо осі, що не проходить через центр мас ланки
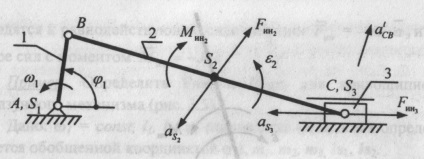
Ріс16. До визначення сил та моментів сил інерції кривошипно-ползунного механізму
Мал. 17. План швидкостей (а) і план прискорень (б) кривошипно-ползунного механізму
Знайдений відрізок відкладаємо від точки в. Щоб знайти абсолютне прискорення центру мас, отриману точку s2 з'єднуємо з полюсом плану прискорень. Тоді.
Сила інерції прикладена в центрі мас S2 і спрямована в протилежний бік від прискорення центру мас (рис. 16).
Для знаходження моменту інерції.
знайдемо кутовий прискорення ланки 2:
Для визначення напрямку # 949; 2 перенесемо вектор тангенціальної складової з плану прискорень на план механізму в точку С. Цей вектор показує напрямок # 949; 2; Мін2 спрямований у протилежний бік.
Ланка 3 робить поступальний рух в направляючих стійки. Сила інерції цієї ланки знайдеться як:
і спрямована в протилежний бік від as3. Мін3 = 0, так як # 949; 3 = 0.
1.5.3 Визначення реакцій в кінематичних парах і врівноважує сили кривошипно-шатунного механізму (рис. 18)
Силове дослідження механізму ведуть за групами Ассура, починаючи його з останньої приєднаної групи Ассура, для якої відомі всі зовнішні сили, і закінчують розрахунок розглядом початкової ланки, на якому потрібно визначити врівноважує силу або момент.
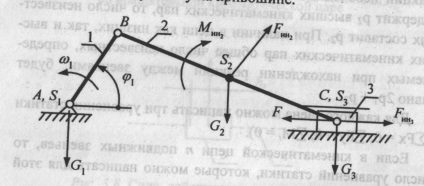
Мал. 18. Силовий розрахунок кривошипно-ползунного механізму
Мал. 19. Реакції, що діють на ланки в групі Ассура другого класу, другого порядку, 2-го виду
Мал. 20. Силовий багатокутник для визначення реакцій, що діють на ланки групи Ассура 2-го виду
При силовому розрахунку за початкову ланку приймають ланка, на якому потрібно визначити Fyp або Мур.
Ланки 2 і 3 утворюють структурну групу Ассура другого класу, другого порядку, 2-го виду, для якої відома зовнішня сила F.
Зобразимо структурну групу ланок 2 -3 в тому ж положенні і в тому ж масштабі, що і на схемі механізму. Покажемо реакції F21 і F30. які замінюють дію відкинутих ланок 1 і 0 (рис. 19).
Складемо таблицю, в яку будемо записувати послідовність визначення реакцій, рівняння, які треба скласти для визначення цих реакцій і номера ланок, для яких записуються ці рівняння.
,
- Для знаходження і складаємо векторне рівняння сил:
Вибираємо масштаб для побудова силового багатокутника:
де аб - довільний вектор зображає в масштабі.
Визначимо відрізки, якими будуть зображувати в масштабі інші сили:
Після цього будуємо замкнутий (тому що # 931; = 0) силовий багатокутник (Рис. 20) в тій послідовності, в якій записані сили, при визначенні # 931; . в результаті чого знайдемо вектори, що зображують шукані реакції. Величини цих реакцій будуть рівні:
Повна реакція буде складатися з її нормальної і тангенціальної складових:
.
Величина сили буде дорівнює: [Н].
Для знаходження реакції складемо векторні рівняння:
.
Перші чотири вектора відповідно до рівняння (3) вже побудовані на рис.20. Тому для визначення величини і напрямку сили з'єднуємо початок вектора з кінцем вектора.
Залежно від виду приводу визначається або урівноважує сила Fyp. або врівноважує момент Мур.
У дослідженні умовно можна прийняти за точку прикладання сили Fyp точку В кривошипа і вважати, що лінія дії цієї сили перпендикулярна кривошипа АВ.
Якщо початкова ланка приводиться в рух через муфту, то визначається Мур.
Варіант 1. Визначення Fyp (рис. 21, а).