Поверхня з позиції кінематичного способу її освіти розглядають як безліч всіх положень рухається лінії (або поверхні). При такому підході до утворення поверхні можна стверджувати, що поверхня буде задана (визначена), якщо в будь-який момент руху утворює будуть відомі її положення і форма, а це, в свою чергу, дозволить однозначно відповісти на питання, чи належить точка простору даної поверхні або немає.
Кінематичний спосіб утворення поверхні підводить нас до поняття визначника, під яким ми будемо мати на увазі необхідну і достатню сукупність геометричних фігур і зв'язків між ними, які однозначно визначають поверхню. У число умов, що входять до складу визначника, повинні бути включені:
1. Перелік геометричних фігур, які беруть участь в утворенні поверхні.
2. Алгоритмічна частина, яка вказує на взаємозв'язок між цими фігурами.
Отже, визначник поверхні складається з двох частин: з сукупності геометричних фігур (перша частина) та додаткових відомостей про характер зміни форми утворює і законі її переміщення (друга частина). Щоб відрізнити першу (геометричну) частина визначника від другої (алгоритмічної) частини, домовимося укладати першу - в круглі, а другу - в квадратних дужках; тоді в загальному випадку визначник поверхні матиме таку структурну форму:
де (Г) - геометрична частина, [Л] - алгоритмічна частина.
Слід мати на увазі, що при завданні поверхні можна в ряді випадків замість геометричних елементів задавати числові параметри. Наприклад, будь-яка сфера буде відрізнятися від всіх інших сфер тільки величиною радіуса R, тому, задаючи число, яке вказує значення R, ми визначаємо одну єдину сферу. Очевидно, числовим параметром конічної поверхні обертання може служити ∠φ ° - кут між твірною і віссю конічної поверхні *.
Параметри поверхні бувають двох видів: параметри форми і параметри положення.
Параметри, зміна яких викликає зміна форми поверхні, називають параметрами форми.
Параметри, зміна яких призводить до зміни положення поверхні в просторі, називають параметрами стану.
Сума умов, що визначають сукупність всіх незалежних параметрів поверхні, називається її параметричних числом.
Параметри форми. У щойно розглянутих випадках параметр R для сфери і ∠φ ° для конічної поверхні відносяться до параметрів форми. Число параметрів, що змінюють форму поверхні, може бути будь-яким цілим позитивним числом, починаючи з нуля. Так, наприклад: число параметрів форми для площині дорівнює нулю; для сфери - одиниці. Якщо поверхня задана свого рівняння в канонічній формі, всі параметри форми входять в це рівняння.
Параметри положення. Число параметрів, що характеризують стан поверхні в просторі, не може бути менше трьох і більше шести. Так, наприклад: для площині воно дорівнює трьом, для тривісного еліпсоїда - шести.
Якщо рівняння, що визначає поверхню, складено для довільного положення поверхні, то воно містить не тільки всі параметри форми, але і всі параметри положення, т. Е. Число незалежних параметрів рівняння в цьому випадку дорівнює параметричного числу поверхні.
Щоб знайти (встановити) визначник поверхні, слід виходити з кінематичного способу її утворення. Так як поверхня може бути утворена різними шляхами, очевидно одна і та ж поверхня може мати різні визначники, наприклад, поверхня прямого кругового циліндра (циліндричну поверхню обертання) з кінематичною точки зору можна уявити:
а) як слід, який залишає в просторі прямої g при її обертанні навколо осі i (рис. 117, а); при цьому визначник циліндричної поверхні обертання буде мати вигляд
* В обох випадках положення поверхні в просторі не враховувалося.
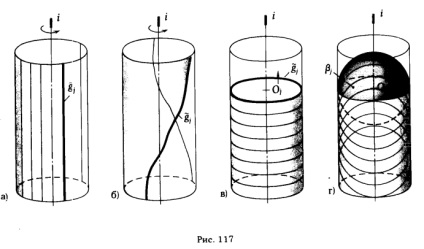
б) як слід від обертання кривої g. що належить поверхні прямого кругового циліндра, навколо осі i (рис. 117,6); в цьому випадку визначник поверхні можна записати:
в) як результат поступального переміщення окружності g. при цьому центр окружності Про переміщається уздовж осі i, а її площину а весь час залишається перпендикулярної до цієї осі (рис. 117, в); тоді визначник поверхні можна записати:
г) як огибающую всіх положень сферичної поверхні β, центр O якої переміщається по осі i (рис. 117, г); визначник в цьому випадку набуде вигляду
З безлічі визначників поверхні зазвичай вибирають найбільш простий; в даному випадку таким визначником буде