Визначення 3. Градієнтом функції в точці називається вектор, який має в стандартному базисі координати. Більш коротке позначення градієнта (значок читається "Набла").
Визначення 4. Нехай. матрицею Якóбі цього відображення в точці називається матриця, що складається з похідних від кожної компоненти по кожній координаті. Похідна по вектору визначається так само, як і раніше.
Визначення 5. Відображення називається диференційовних в точці, якщо його повний приріст може бути представлено у вигляді
, де - лінійний оператор, тобто відображення, що володіє властивістю лінійності:. Оператор діє з простору в простір. Він називається похідним відображенням і позначається. Вираз або називається диференціалом і позначається. Очевидно, що з дифференцируемости слід безперервність.
Теорема 1. (Необхідна умова дифференцируемости). Якщо відображення диференційованою в точці, то в цій точці існують всі приватні похідні і навіть похідні з будь-якого вектору. При цьому . Однак, на відміну від випадку функцій однієї змінної, з існування похідної по будь-якому вектору не слід дифференцируемость відображення.
Доведення. Нехай. тоді
Тому. Відсутність зворотного імплікації видно, наприклад, з наступного контрпримера.
Контрприклад. Нехай. У цій функції існує похідна в точці з будь-якого вектору і ця похідна дорівнює. Якби функція була диференційованою в точці, вираз лінійно залежало б від вектора. Тобто було б. Однак, не завжди. Так, наприклад, або.
Слідство. Якщо відображення диференційованою в точці, то в цій точці існують всі приватні похідні, а матрицею лінійного
оператора в стандартному базисі є матриця Якобі.
Доведення*. Позначимо матричні елементи в базисі. Тоді буде.
Теорема 2. (Достатня умова дифференцируемости). Якщо все приватні похідні існують в околиці точки і безперервні в самій точці, то відображення диференційованою в цій точці.
Доведення. Досить при зазначених умовах довести дифференцируемость скалярної функції, тобто однієї компоненти відображення. Метод докази простіше зрозуміти в разі. Ми маємо
, де число укладено між числами, а укладено між числами (теорема Лагранжа).
Якщо прагнуть до нуля, то також прагнуть до нуля. Скориставшись безперервністю похідних і в точці, отримаємо. Ч і т.д.
1 о. Розглянемо скалярний поле, тобто функцію. Якщо функція f диференційовна в точці, то, як ми вже знаємо,. У нашому випадку це означає, що
Так як напрямні косинуси вектора рівні, то вектор одиничної довжини дорівнює. Ми отримуємо формулу для обчислення похідної за напрямком:
Нерівність Коші показує, що. Рівність тут можливо лише, якщо вектори і колінеарні. Таким чином, похідна по напрямку приймає найбільше значення, якщо коллінеарен вектору. Так само це найбільше значення. Звідси випливає, що градієнту можна дати нове (бескоордінатное) визначення.
Визначення. Градієнт функції в точці - це вектор, довжина якого дорівнює найбільшою з похідних по всіляких напрямках в точці. Напрямок градієнта збігається з напрямком найбільш швидкого зростання функції в цій точці.
Ми бачимо, що градієнт скалярного поля (функції) не залежить від вибору координат, а визначається самим полем.
Відзначимо, що за напрямом "мінус градієнта" функція швидше за все убуває, а за напрямками, перпендикулярним до градієнту, функція має нульову швидкість зміни, так як, якщо, то.
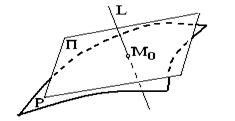
2 о. Розглянемо поверхню, задану неявним рівнянням, де дифференцируема в точці, що лежить на цій поверхні, причому градієнт відмінний від нуля в цій точці (така точка називається регулярною). Всі прямі, що проходять через цю точку і перпендикулярні вектору, лежать в одній площині, яка називається дотичній площиною до поверхні в точці. Рівняння дотичної площини має вигляд
Наведемо ще канонічні рівняння нормалі (тобто прямий, яка перпендикулярна площині і також проходить через точку):
Нехай рівняння поверхні приведено до явного виду, де функція диференційована в точці. Якщо прийняти, то ми знову повернемося до рівняння. Зараз, тому рівняння дотичної площини набуде вигляду
де (порівняйте з рівнянням дотичної до графіка).
Ясно, що, коли. Таким чином, дотична площину в околиці точки прилягає до поверхні тісніше, ніж будь-яка інша площина.
Рівняння нормалі зараз набувають вигляду
Приклад. Скласти рівняння дотичної площини і нормалі до еліпсоїда в точці.
Рішення. Перш за все, т. Належить даній поверхні, тому що .
1-й спосіб. Оскільки , То,. Можна вважати, що нормальний вектор дотичної площини дорівнює.
Тому отримуємо рівняння і.
2-й спосіб. . Отже,,,. Тому рівняння дотичної площини має вигляд: або, а канонічні рівняння нормалі:.
Вправа. Довести, що рівняння дотичної площини до еліпсоїда з рівнянням в точці, що лежить на цій поверхні, має вигляд.
Генерація сторінки за: 0.008 сек.