Середня арифметична має ряд математичних властивостей, які можна використовувати, щоб спростити її розрахунки. Основні властивості середньої арифметичної такі.
1. Середня арифметична постійної величини дорівнює цій постійній:
2. Сума квадратів відхилень від середньої арифметичної завжди менше, ніж сума квадратів відхилень від будь-якої іншої величини:
3. Величина середньої не зміниться, якщо частоти ряду розподілу замінити частостей.
4. Сума відхилень окремих значень ознаки від середньої, перемноження на ваги (частоти), дорівнює нулю:
£ (х - х) = х - пх = 0 - для простої середньої;
5. Якщо всі значення ознак збільшити або зменшити в однакове число раз (к), то середня (х) збільшиться чи зменшиться в стільки ж разів:
тобто середня зменшилася в (к) раз.
6. Якщо з усіх значень варіант (х) відняти або додати до них ту ж постійну величину (х0), то середня (х) зменшиться або збільшиться на таку ж величину (хо):
тобто середня зменшилася на постійне число х0.
7. Якщо частоти (ваги) розділити або помножити на якесь постійне число (к), то середня не зміниться:
тобто значення середньої не змінилося.
8. Твір середньої на суму частот дорівнює сумі творів варіант на частоти:
Це рівність випливає з визначальною властивості середньої арифметичної, згідно з якою, порівнюючи варіанти, надаючи їм однакові значення шляхом заміни їх середнім значенням, незмінним залишається загальний обсяг ознаки.
9. Загальна середня дорівнює середній з приватних середніх, зважених за чисельністю відповідних частин (груп) сукупності:
Викладені вище властивості середньої арифметичної дозволяють спростити її розрахунки: можна з усіх значень ознаки відняти довільну постійну величину, отриману різницю розділити на величину інтервалу, а потім обчислену середню помножити на величину інтервалу і додати довільну постійну величину, яка прийнята за початок відліку.
Формула обчислення середньої арифметичної спрощеним способом має такий вигляд:
де х = --уменьшена середня арифметична;
х = х до ° - відхилення в інтервалах; х0 - початок відліку;
до - величина інтервалу.
Середня х з значення - називається моментом першого порядку, а до спосіб обчислення середньої способом моментів або способом відліку від умовного початку.
За умовне початок відліку (х0) зазвичай приймають одне із значень варіючої ознаки, яке, як правило, знаходиться в центрі ряду розподілу або таке, яке має найбільшу частоту.
Розглянемо приклад визначення середньої арифметичної в інтервальному ряду розподілу способом моментів, використовуючи дані про розподіл 100 господарств по надою молока на корову (табл. 4.7).
За умовне початок відліку (х0) візьмемо одне зі значень інтервалу, розташованого в центрі ряду розподілу та яке має найбільшу частоту. У нашій задачі таким значенням х0 = 33 ц. Величина інтервалу к = 2 ц.
За даними таблиці визначимо умовну (зменшену) середню арифметичну:
Таблиця 4.7. Дані для розрахунку середньої арифметичної в інтервальному ряду розподілу способом моментів
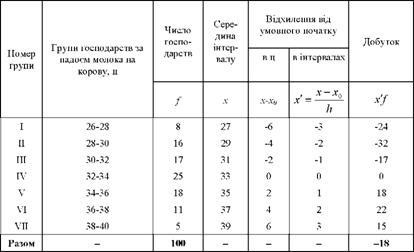
Щоб отримати дійсну середню продуктивність корів, необхідно внести відповідні поправки:
Таким чином отримано такий же результат як і за даними табл. 4.2. Результати розрахунків середньої арифметичної двома способами повністю збіглися.