Нехай є характеристичне рівняння замкнутої системи
Для визначення того, в якому діапазоні можуть змінюватися параметри a1 ... an при стійкій роботі системи, був розроблений і вдосконалений (1940 А.А. Соколов, 1948 М. Ю. І. Неймарк) метод виділення областей стійкості.
Нехай є - годограф Михайлова на кордоні стійкості. Якщо система знаходиться на межі стійкості, то годограф Михайлова D (jv) проходить через початок координат, що може бути відображено рівнянням:
Виділимо в рівнянні (6.45) потрібні параметри і накреслив кордон при v = 0¸¥. Ця межа називається D-розбиттям і являє собою відображення кордону стійкості в площині коренів в площині параметрів системи.
Малюнок 6.26 D-розбиття
Щоб система була стійка, необхідно, щоб всі корені характеристичного рівняння замкнутої системи були «лівими».
Коефіцієнти характеристичного рівняння залежать від постійних часу
Для з'ясування характеру впливу параметрів на стійкість переносять кордон стійкості із площини коренів в площину параметрів. Це роблять з умови Dз (jv) = 0. У цьому рівнянні виділяють параметри і будують в площині параметрів кордон стійкості (криву D-розбиття).
Кордон стійкості виділяється штрихуванням за правилом Неймарка. При русі по уявної осі від w = - ¥ до w = + ¥ штрих ліва сторона, залишаючи область коренів з негативною дійсною частиною зліва.
Маємо: - характеристичне рівняння замкнутої системи. Необхідно знайти рівняння кордону стійкості, тобто при - ¥ D-розбиття для одного комплексного параметра. 1) Записуємо. тобто з полінома D (p) виносять параметр K. а S (p) - поліном, що не містить параметр K. 2) Далі - поділяємо на речову та уявну частини. 3) Будуємо залежність K (v). здався різними значеннями v. Отримаємо кордон областей стійкості. 4) Виділяємо області стійкості штрихуванням по Неймарк, для цього: а) відзначаємо напрямок руху v від - ¥ до + ¥; б) заштриховуєш ліву частину кривої по відношенню до руху. Вся площина розбивається на три зони (I, II і III) (рисунок 6.27). Частина площини, в бік якої спрямовані штрихи (I зона) відображає ліву полуплоскость коренів і тому має найбільшу кількість лівих коренів і є областю найбільшої стійкості.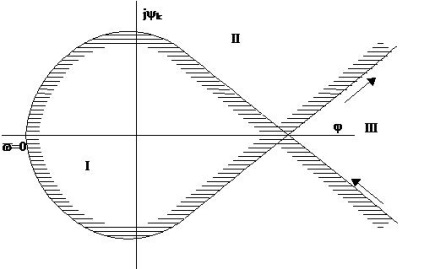
Малюнок 6.27 Кордон областей стійкості.
Переходячи з I в II область, тобто переходячи криву D-розбиття з заштрихованої частини в НЕ заштрихованную, втрачається один негативний і купується один позитивний корінь (корінь переходить в праву полуплоскость).
Запас стійкості зменшується в III області, де втрачається два негативних кореня.
Отже, область I (рисунок 6.27) має найбільший запас стійкості. Перевіряємо стійкість в точці 0. Так як параметр K - речовинний, то знаходимо ті значення K. які знаходяться в I області на дійсній осі. При цих значеннях САР буде володіти найбільшим запасом стійкості.
Приклад. Характеристичне рівняння замкнутої системи:
Знайдемо значення K, відповідне найбільшої стійкості.
4) так як параметр k-речовинний, то речові значення k = j (v) і лежать на відрізку AB, тобто від -1 до 19.8 відповідають усталеній роботі САР.
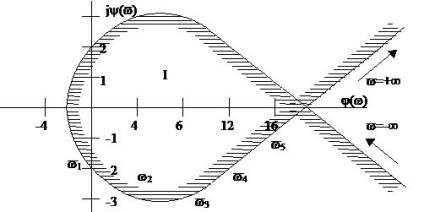
Малюнок 6.28 Приміром визначення найбільшої стійкості замкнутої системи
Часто буває, що областей з різними областями стійкості менше ступеня характеристичного рівняння, а значить і числа коренів характеристичного рівняння. В такому випадку область найбільшої стійкості дають тільки запас стійкості, але не відповідає на питання, стійка чи система, при цьому необхідно після вибору параметрів досліджувати стійкість іншими методами.
Найчастіше це роблять при значенні параметра дорівнює нулю, тобто на початку координат кривої D-розбиття.
У нашому характеристичний рівнянні покладемо k = 0.
і знайдемо коріння, що прирівнюють до нуля всі співмножники
тобто I-я область відповідає усталеній роботі САУ при зміні k від -1 до 19,8, тобто від 0 до 19,8.
Для визначення абсолютного числа негативних коренів для якогось приватного значення досліджуваного параметра треба вирішити характеристичне рівняння і знайти число цікавлять нас коренів. Зазвичай величина параметра береться рівною нулю (початок координат площині параметра). При цьому характеристичне рівняння спрощується. Надалі ми визначаємо число коренів у всіх зонах за допомогою штрихування на кривій D-розбиття.
Вибираємо область найбільшої стійкості і порівнюємо кількість негативних коренів з показником ступеня n характеристичного рівняння. Якщо кількість негативних коренів одно n, то система стійка.