Нехай довільна замкнена лінія l пронизує провідник зі струмом (рисунок 1), тобто вони зчіплюються один з одним як дві ланки ланцюга. Навколо провідника виникає магнітне поле.
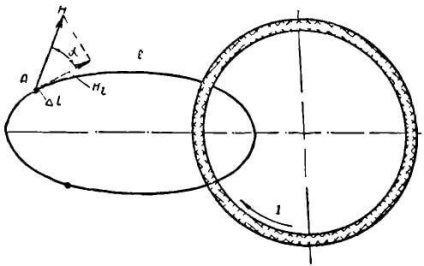
Малюнок 1. Закон повного струму
Побудуємо вектор напруженості H. створюваної струмом в точці А. розташованої на лінії l. Якщо лінія охоплює кілька провідників зі струмом, то для кожного струму будуються вектори напруженості в даній точці лінії. Складаючи геометрично окремі вектори напруженості, знаходимо вектор результуючої напруженості магнітного поля.
Вектор результуючої напруженості H в загальному випадку утворює з елементом довжини # 916; l кут # 945 ;. Тому поздовжня або тангенціальна складова Hl результуючої напруженості H буде:
Якщо розбити замкнуту лінію на n елементів довжини і скласти твори довжин всіх елементів на тангенціальні складові результуючої напруженості в цих елементах, отримаємо таку суму:
Цю суму можна змалювати таку картину:
де знак означає суму від k = 1 до k = n.
У теоретичній електротехніці доводиться, що зазначена сума дорівнює сумі алгебри струмів, зчіпних з контуром підсумовування подібно до того, як зчіплюються між собою два суміжних ланки ланцюга.
Отже, можна записати так:
Це формулювання називається законом повного струму. Для випадку, коли контур багаторазово пронизує один і той же виток, як, наприклад, при наявності обмотки з числом витків w. повний струм буде:
Якщо замкнутий контур підсумовування збігається з магнітною лінією, то вектор напруженості в будь-якій точці контуру буде спрямований по дотичній до елементу довжини # 916; l.
і закон повного струму набуває вигляду:
Якщо значення напруженості для всіх точок контуру при цьому однаково, а сума # 916; l по контуру дорівнює l. то формула закону повного струму запишеться так:
Закон повного струму є основним законом при розрахунку магнітних ланцюгів і дає можливість в деяких випадках легко визначати напруженість поля.
Наприклад, застосовуючи закон повного струму для визначення напруженості на відстані a від прямолінійного провідника зі струмом, маємо:
Малюнок 2. До визначення напруженості поля котушки, намотаною на кільце
Щоб визначити напруженість поля всередині котушки, намотаною на кільце (малюнок 2), скористаємося знову законом повного струму. Контуром тут є коло радіуса r. Контур пронизує w витків з струмами одного напрямку:
Позначаючи довжину середньої лінії кільця через l = 2 × π × r. отримуємо:
Таким чином, напруженість поля котушки пропорційна добутку числа ампер на число витків або числу ампер-витків. I × w називається намагничивающей силою і позначається буквою F. Оскільки w - число абстрактне, то сила, що намагнічує вимірюється в амперах.
Магнітна індукція всередині котушки буде:
Якщо площа поперечного перерізу кільця по всій довжині однакова і дорівнює S. то, знаючи магнітну індукцію B. можна визначити магнітний потік Ф:
Цю ж формулу можна представити в іншому вигляді:
За своєю будовою ця формула нагадує формулу Ома. Вище було зазначено, що твір I × w називається намагничивающей силою. Вираз стоїть в знаменнику, називається магнітним опором і позначається буквою Rм:
З цієї формули видно, що магнітне опір пропорційно довжині шляху і обернено пропорційно перетину матеріалу, по якому проходить магнітний потік.
Таким чином, магнітний потік Ф пропорційний силі, що намагнічує F і обернено пропорційний магнітному опору Rм:
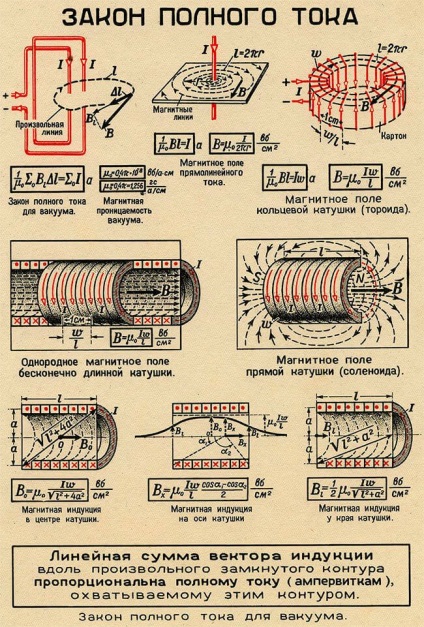
Малюнок 3. Закон повного струму для вакууму
Джерело: Кузнецов М.І. "Основи електротехніки" - 9-е видання, виправлене - Москва: Вища школа, 1964 - 560с.