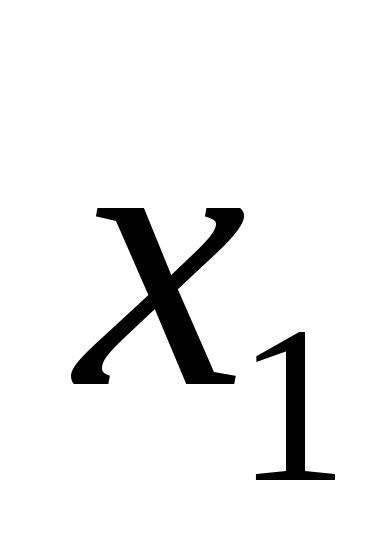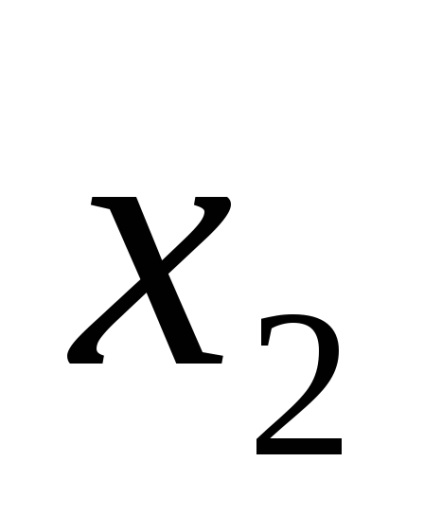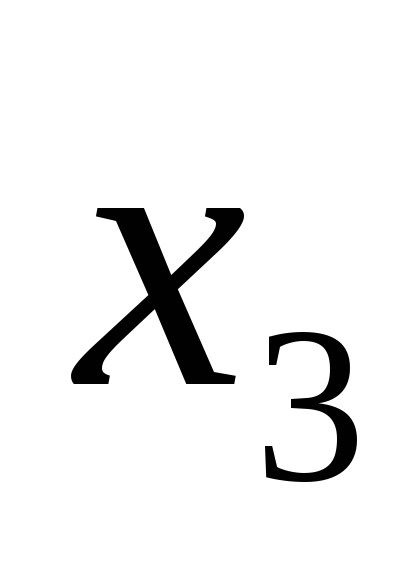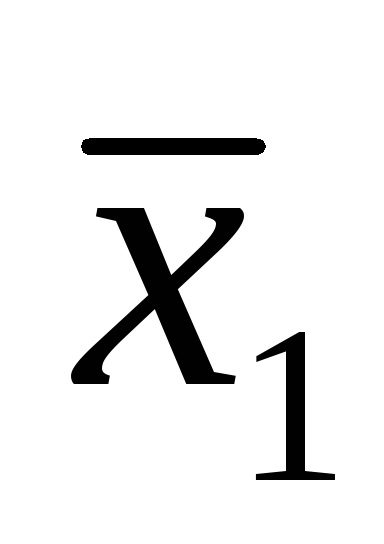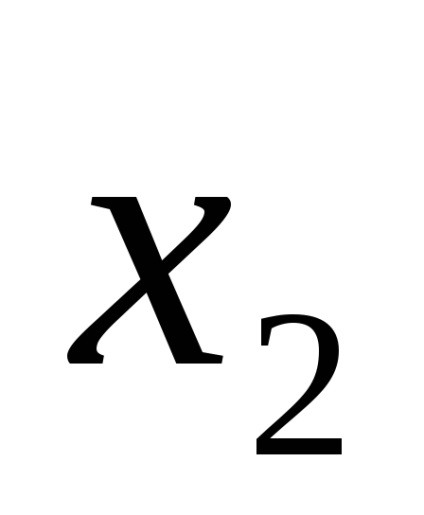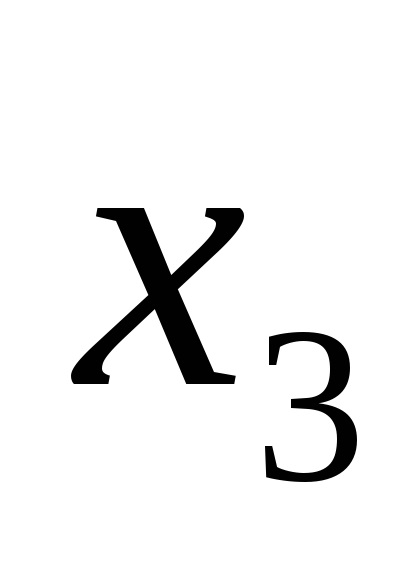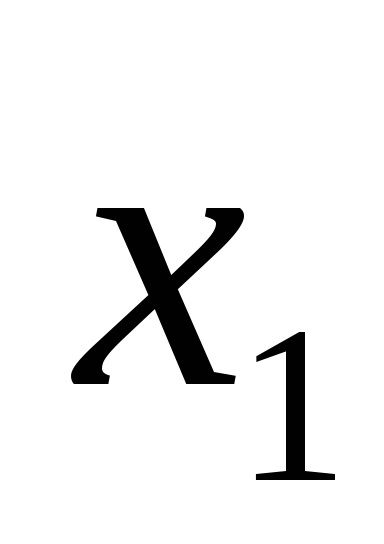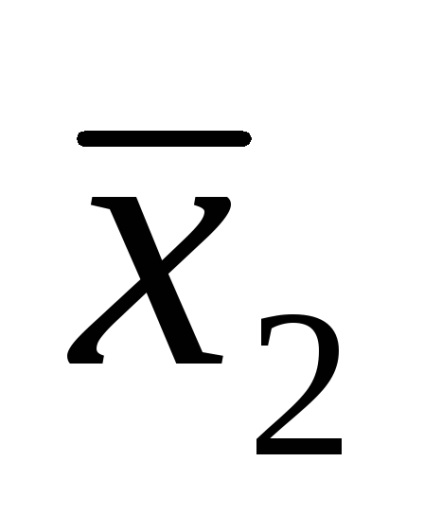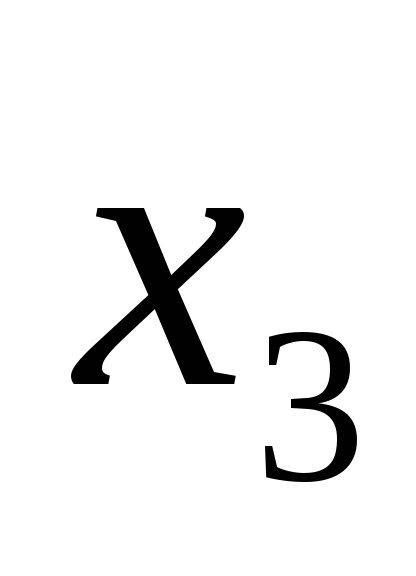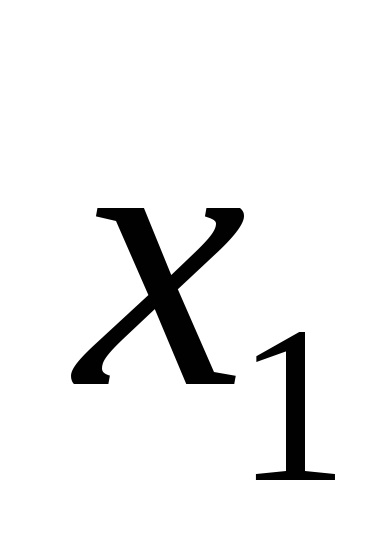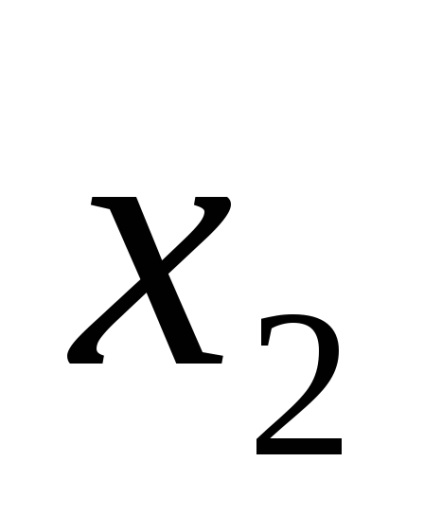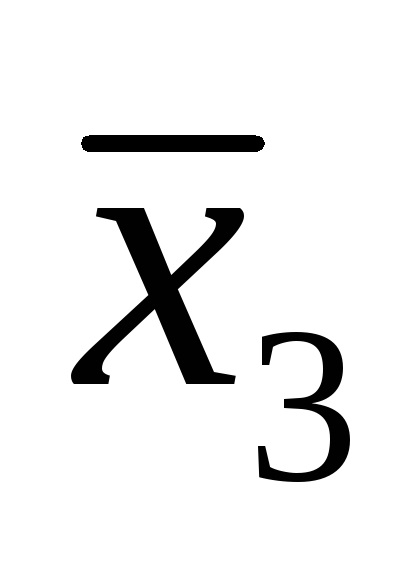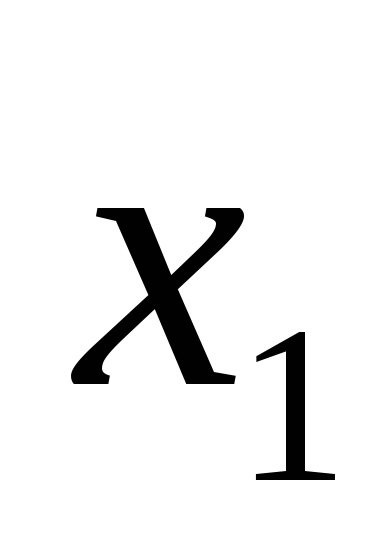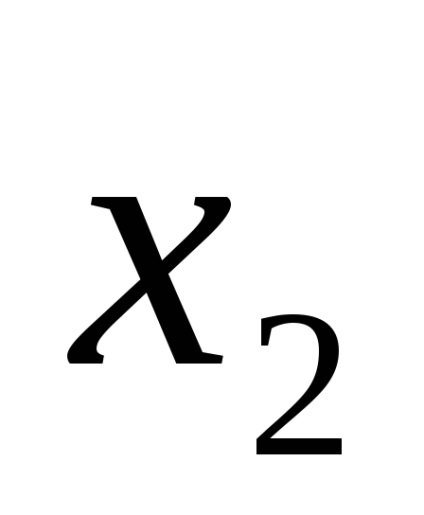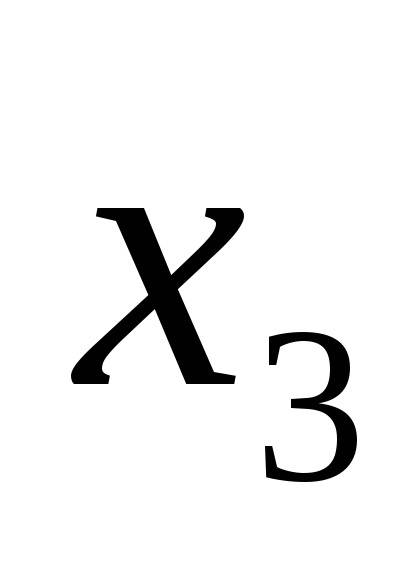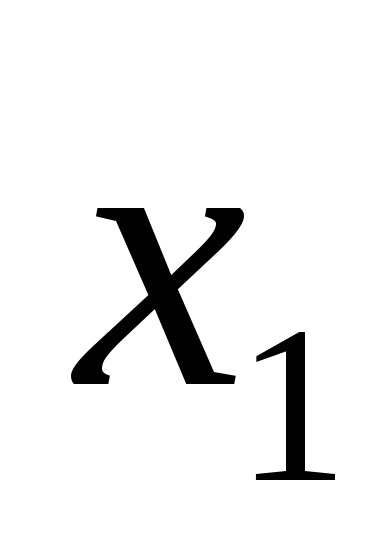Форми логічних функцій
Одна і та ж логічна функція може бути записана по-різному. Наприклад, функція F (
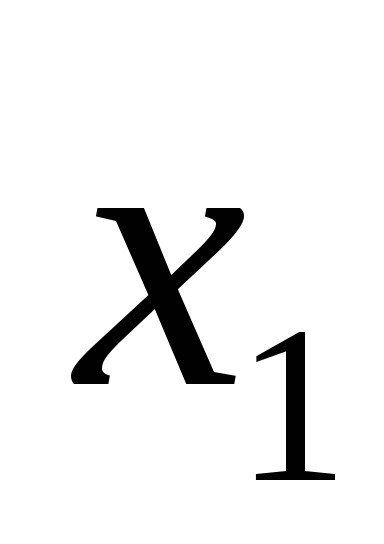
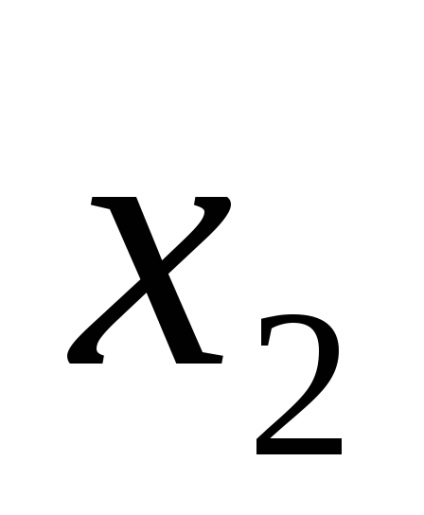
Еквівалентність вираження легко перевірити підстановкою в них значень
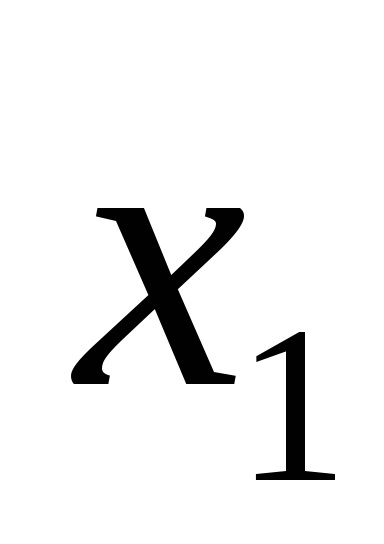
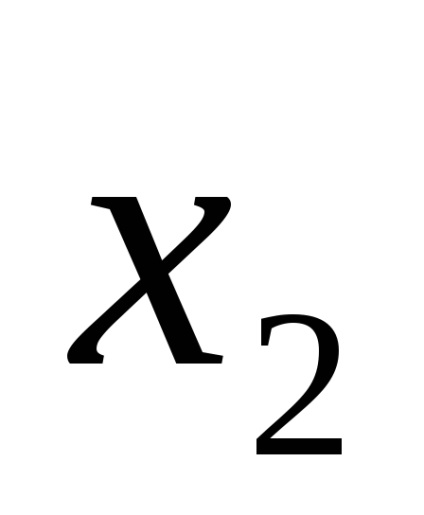
Елементарної називається кон'юнкція, в яку входять тільки змінні і їх заперечення.
Елементарної називається диз'юнкція, що представляє собою логічну суму змінних і їх заперечень.
В елементарні кон'юнкції (диз'юнкції) не можуть входити однакові змінні, а також змінні з їх запереченнями. Такі диз'юнкції (кон'юнкції) повинні перетворюватися. При цьому вони спрощуються, а також перетворюються в 0 або 1.
Правильність перетворень може бути перевірена підстановкою значень змінних. Елементарна кон'юнкція (диз'юнкція) може характеризуватися рангом, що дорівнює кількості змінних в кон'юнкції (диз'юнкції). Поняття елементарної кон'юнкції і диз'юнкції дозволяють досить просто визначити діз'юнктівную і кон'юнктівную форми запису логічних функцій.
Диз'юнктивна нормальна форма (ДНФ) - це форма, в якій логічна функція представляється у вигляді диз'юнкції елементарних кон'юнкція, наприклад: F =
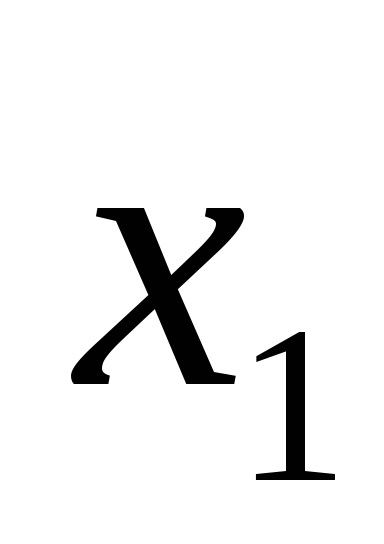
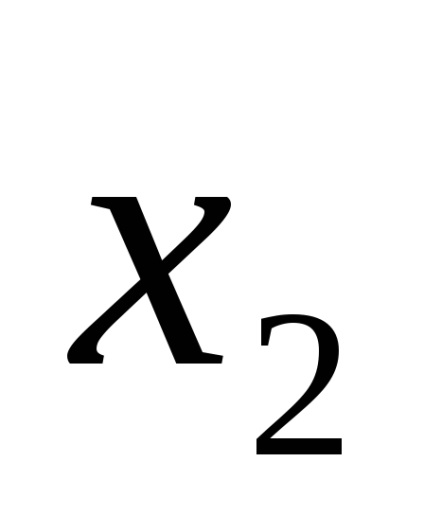
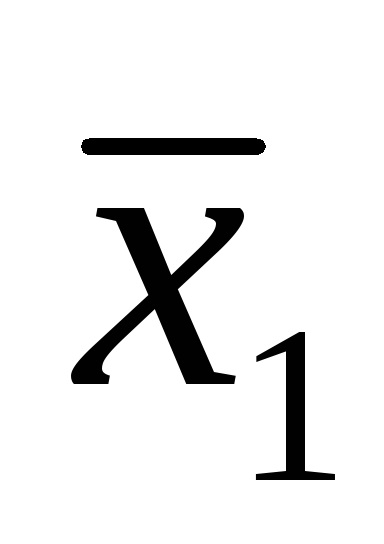
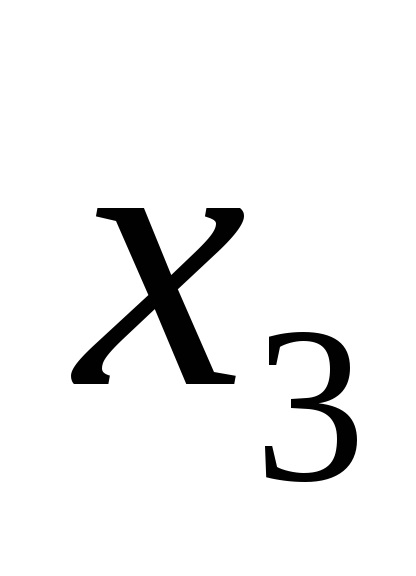
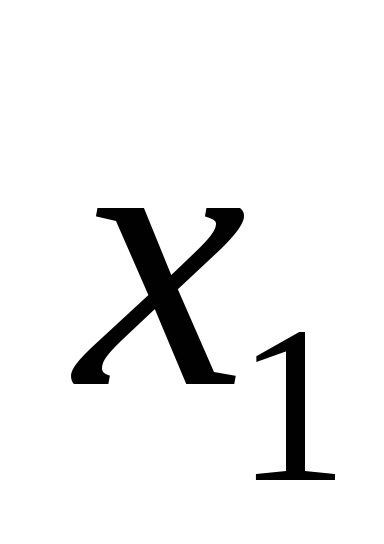
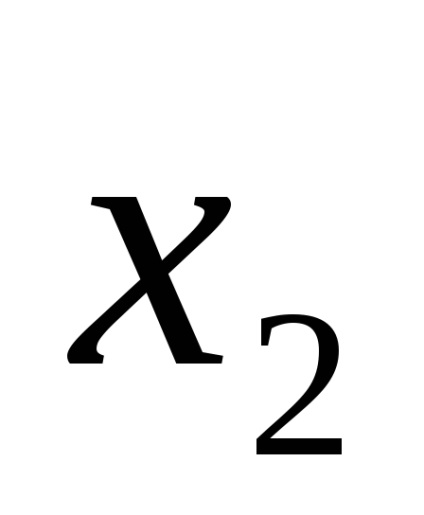
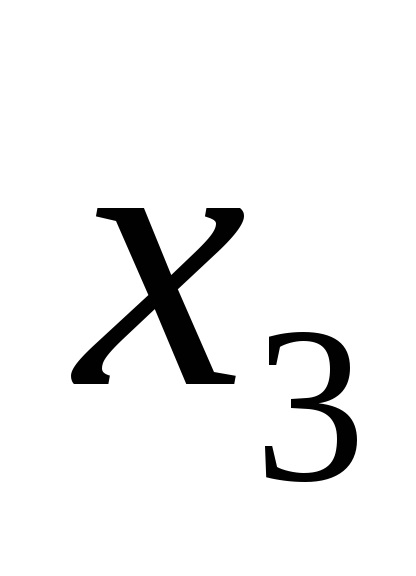
Функції виразів (1) і (2) записані також в ДНФ.
Кон'юнктівной нормальною формою (КНФ) називається така форма, в якій функція представляється у вигляді кон'юнкції елементарних диз'юнкцій, наприклад: F = (
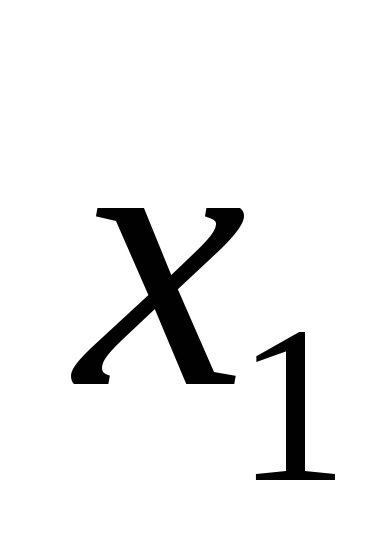
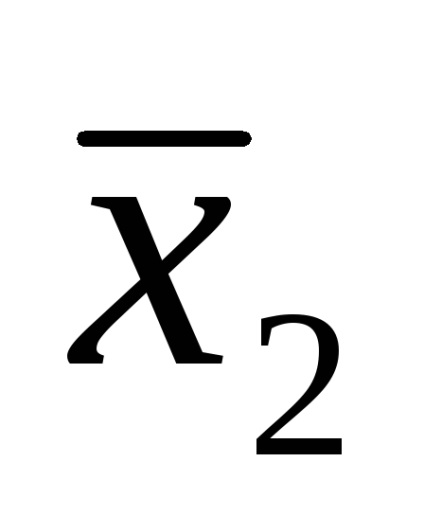
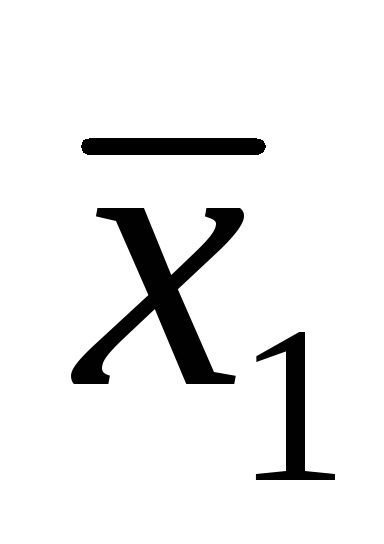
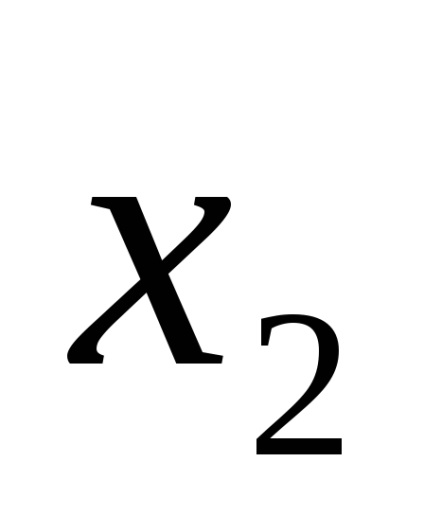
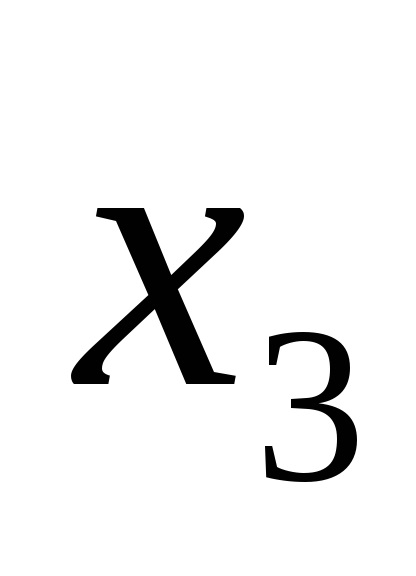
Використання нормальних форм не усуває повністю неоднозначності записи логічних функцій. Наприклад, функція (4) може бути записана також виразами:
Тому серед нормальних форм виділяються такі, в яких функції записуються єдиним чином. Їх називають досконалими. Застосовуються досконала діз'юнктівная ісовершенная Кон'юнктивна нормальні форми (СДНФ і СКНФ). Форми СДНФ і СКНФ мають дві відмінні риси:
всі елементарні кон'юнкції і диз'юнкції мають однаковий ранг;
в елементарні кон'юнкції (диз'юнкції) входять всі ті змінні або їх заперечення, від яких залежить функція.
Функція (5) містить кон'юнкції однакового рангу, але записана в ДНФ, а не в СДНФ. Це пояснюється тим, що елементарні кон'юнкції не містять всіх тих змінних або їх заперечень, від яких залежить функція.
Функція F (
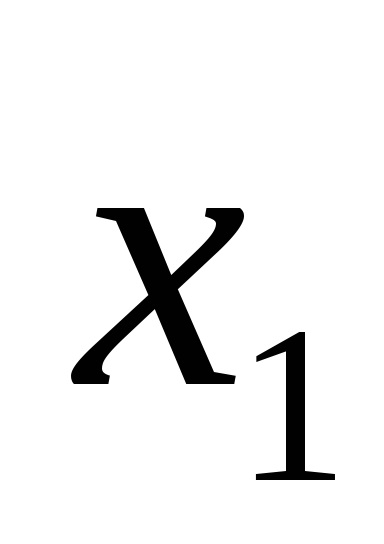
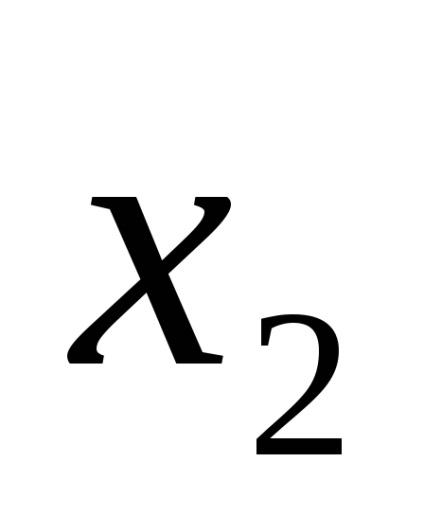
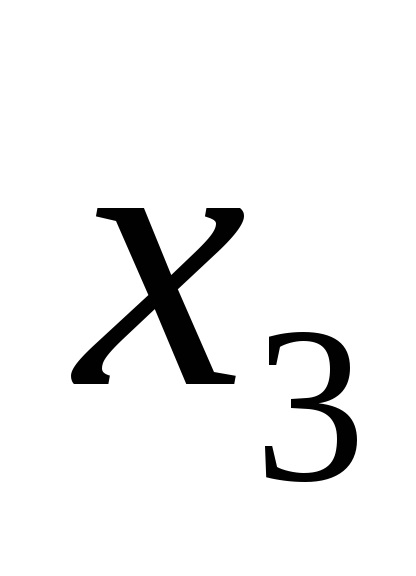
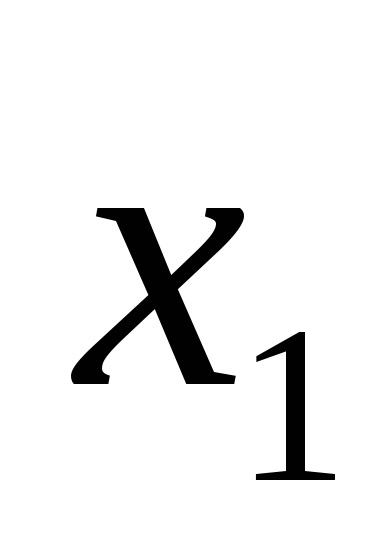
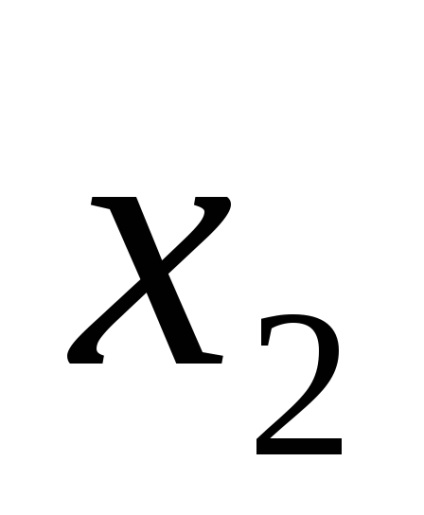
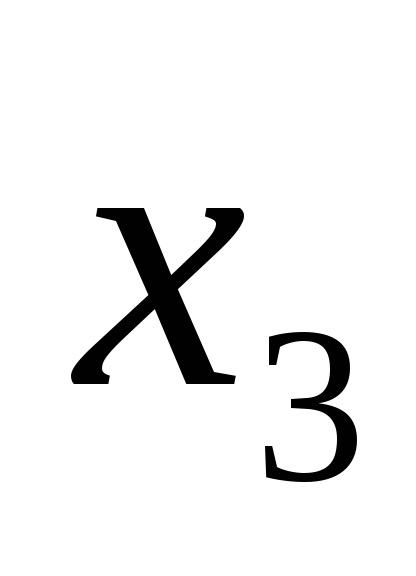
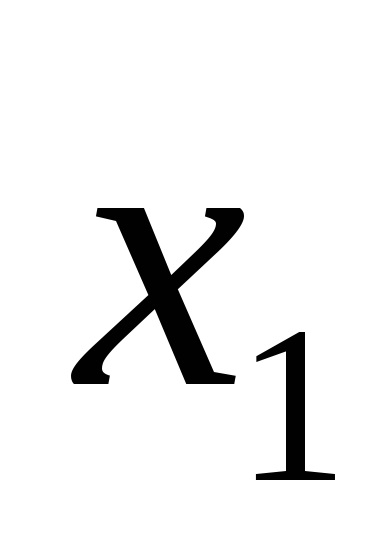
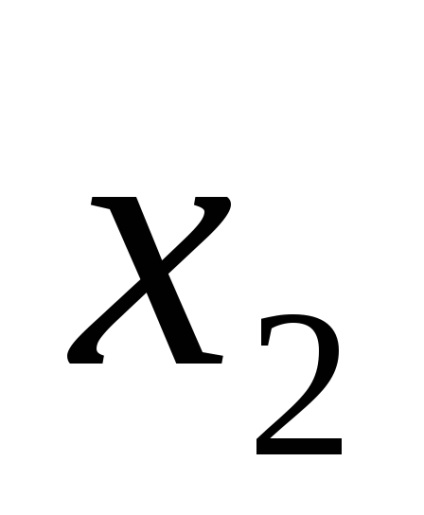
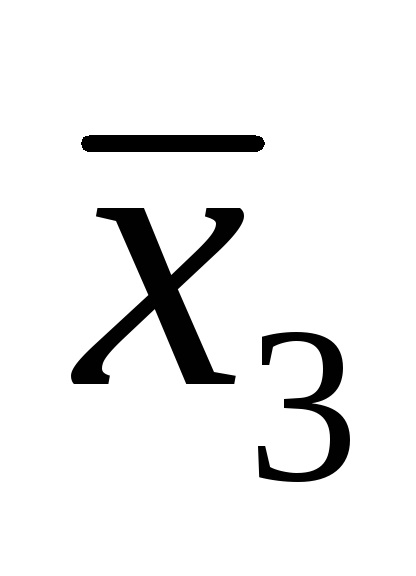
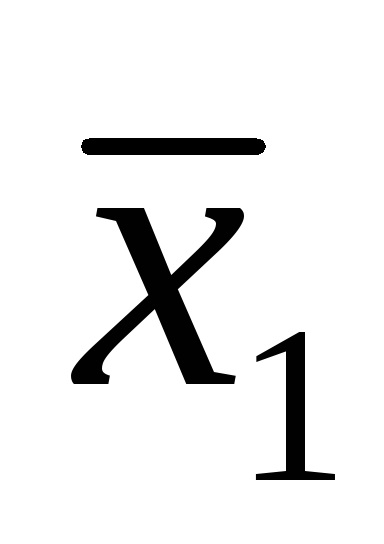
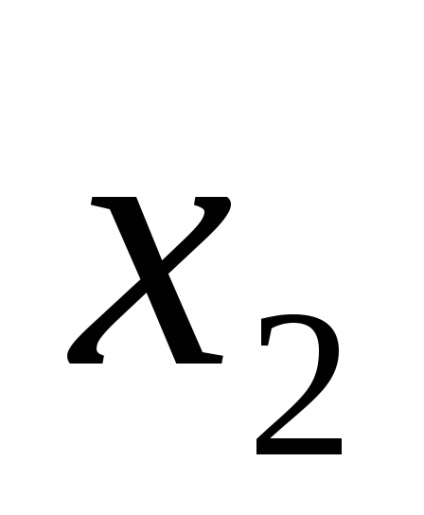
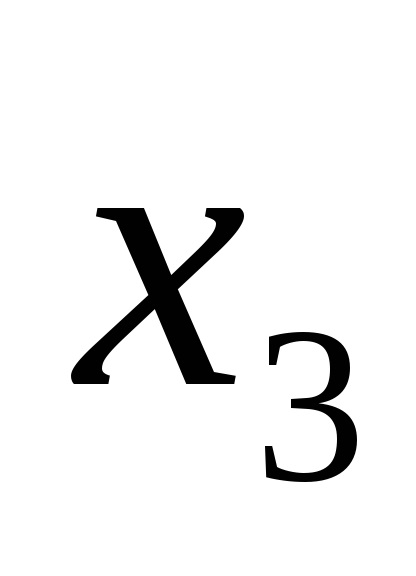
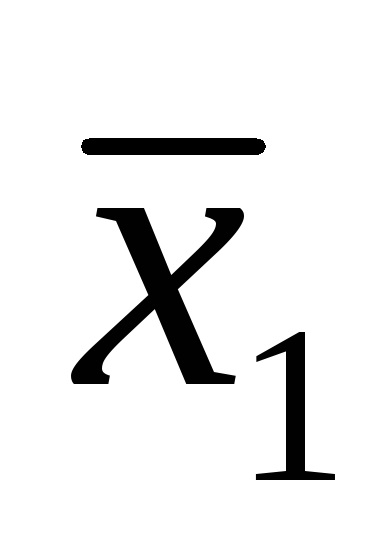
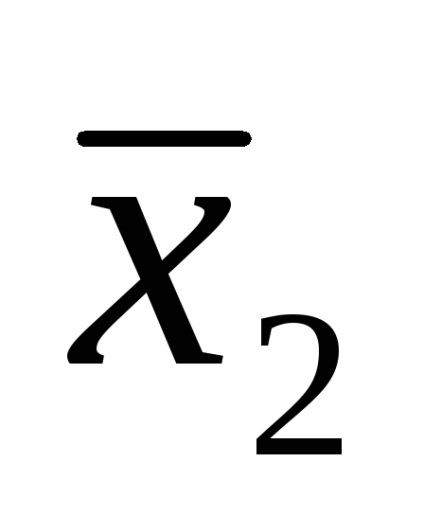
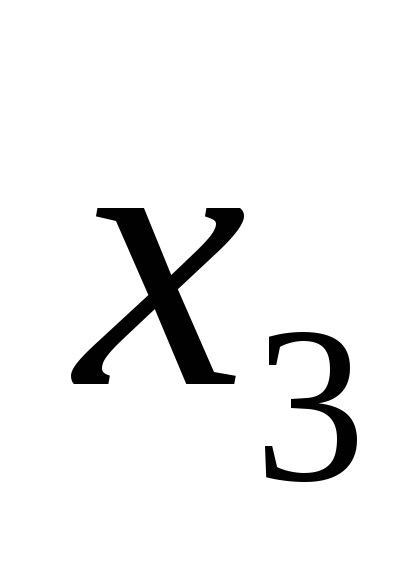
Функція в СДНФ і СКНФ зазвичай записуються за таблицями істинності за певними правилами.
1 .Право записи СДНФ функції по таблиці істинності:
Для всіх наборів змінних, на яких функція приймає одиничні значення, записати кон'юнкції, інвертуємо ті змінні, яким відповідають нульові значення. Потім кон'юнкції з'єднати знаками диз'юнкції.
Наприклад, логічна функція задана таблицею істинності, представленої на рис. 9а. Для наборів 3, 5, 6, 7 записуємо кон'юнкції через пробіл:
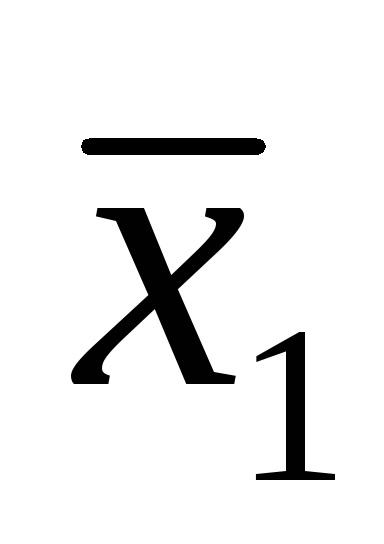
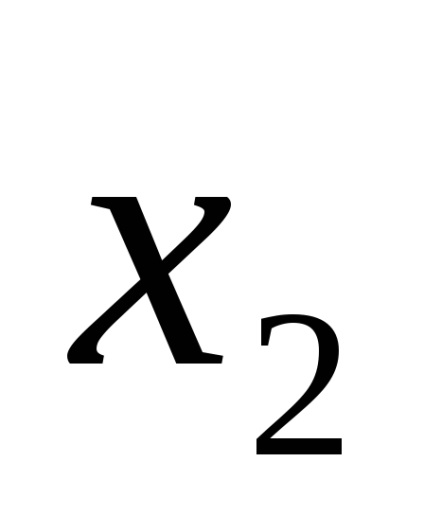
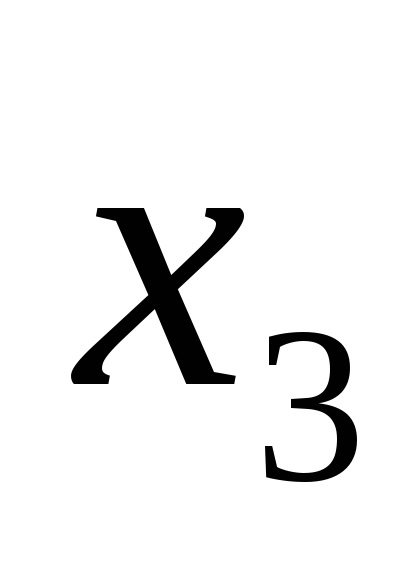
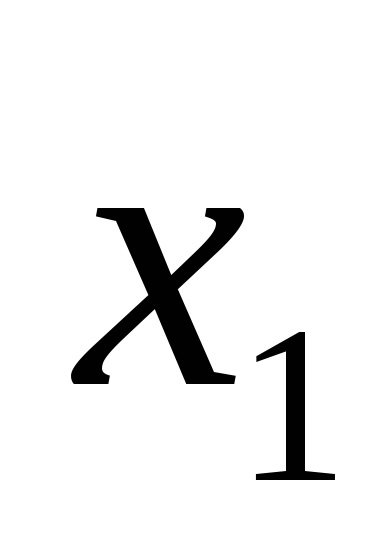
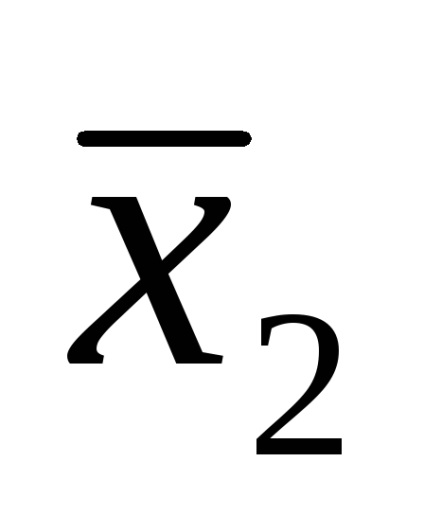
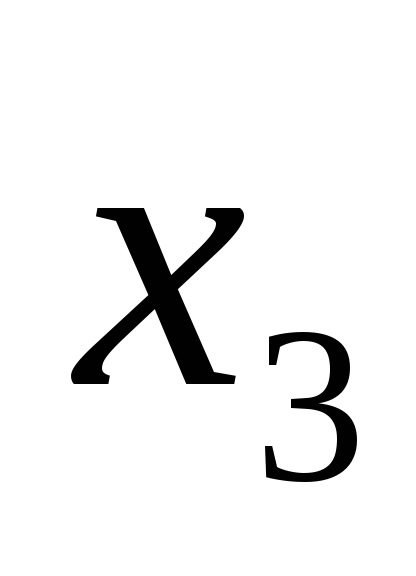
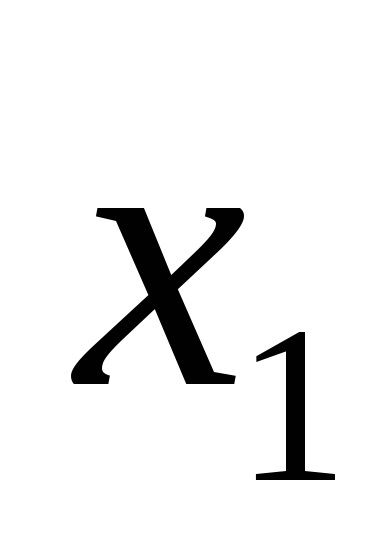
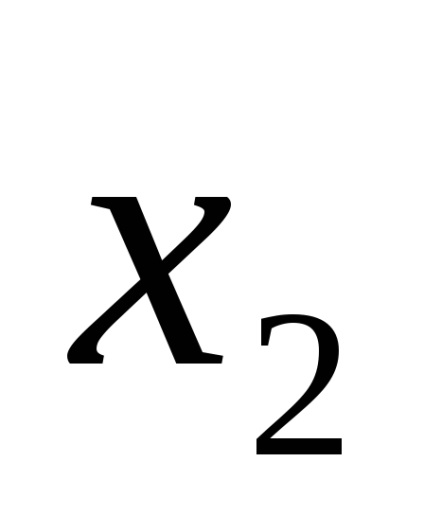
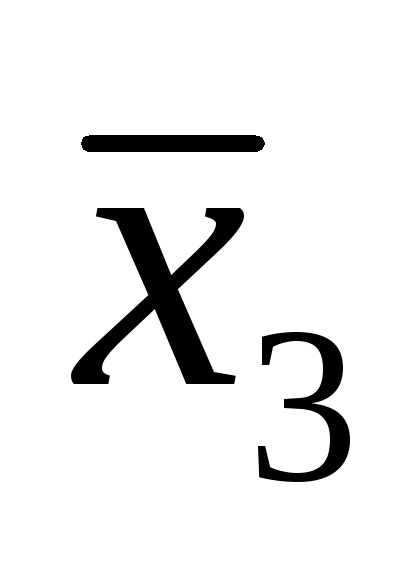
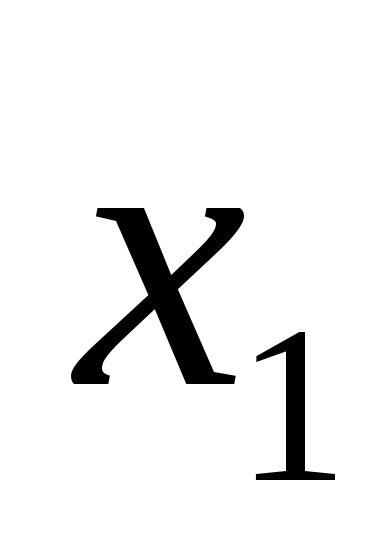
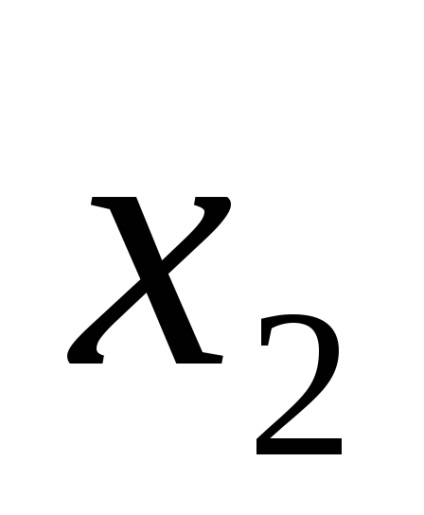
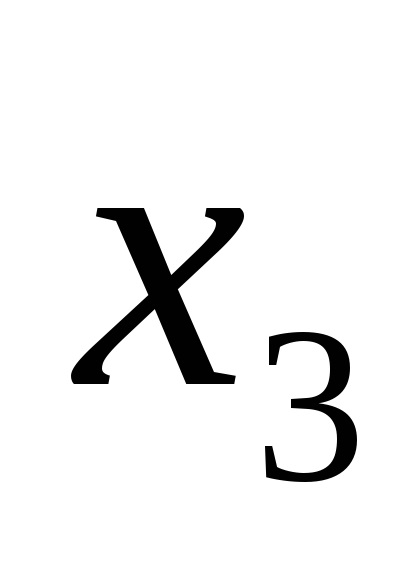
У прогалини ставимо знак диз'юнкції і отримуємо функцію в СДНФ, тобто F (