Головна nbsp> nbsp Wiki-підручник nbsp> nbsp Математика nbsp> nbsp10 клас nbsp> nbspПрімененія безперервності: метод інтервалів і приклади
Функція називається неперервною в точці х0, якщо f (x) прагне до f (x0) при прагненні x до x0. При цьому f (x) - A = f (x) - f (x0) = Δf. Якщо функція f неперервна в кожній точці деякого проміжку А, то ця функція буде неперервною на всьому проміжку А. А сам проміжок А, називають в такому випадку проміжком безперервності функції f.
Графік безперервних функцій, що вивчаються в шкільному курсі математики, можна намалювати «не відриваючи олівець від паперу», так як він є суцільну лінію. Якщо на деякому інтервалі (a; b) функція f неперервна і не звертається в нуль, то на цьому інтервалі вона буде зберігати постійний знак.
Це властивість дуже легко для розуміння. Функція, розташована вище осі Ох, має знак «плюс», функція, розташована нижче осі Ох, має знак «мінус». Якщо лінія функції не перетне вісь Ох (на осі Ох функція дорівнює нулю), то вона явно не змінить свій знак.
метод інтервалів
Одним з яскравих застосувань властивостей безперервності функцій є метод інтервалів, який використовується для вирішення нерівностей з однією змінною. Нехай деяка функції неперервна на інтервалі А і звертається в нуль в кінцевому числі точок належать цьому інтервалу.
Використовуючи властивість, наведене вище, ці точки будуть розбивати весь інтервал А на проміжки, в яких функція буде зберігати свій знак. Щоб визначити знаки всіх проміжків, досить знати знак одного будь-якого з цих інтервалів.
Приклад функції, яка не є безперервною
До сих пір ми стикалися тільки з безперервними функціями. Але існують функції, які не є безперервними в кожній точці, в якій вони визначені. Наприклад, функція f (x) =, де - є дрібна частина числа х. Її графік зображений на наступному малюнку.
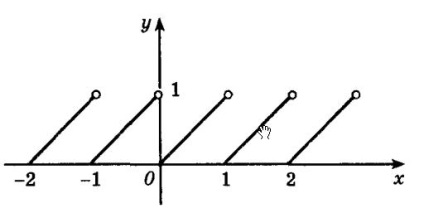
Легко помітити, що основна властивість безперервності функції в точці х0 дорівнює будь-якому цілому числу, не виконуватиметься. Але в той же час функція f (x) = неперервна в усіх інших точках, на яких вона визначена, крім точок, де x дорівнює цілому числу. На графіку такі точки відзначені виколотими кружками.
Функції безперервні, але не диференціюються в даній точці
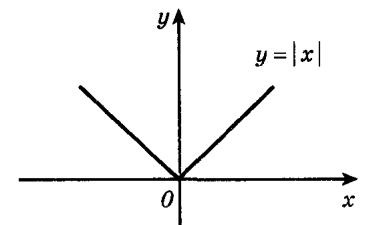
Є функції які є безперервними в кожній точці своєї області визначення. Але при цьому не матимуть похідні в деяких точках. Наприклад, функція y = | x | неперервна на все числової осі, але при цьому не диференційована в точці х = 0. Нижче представлений графік цієї функції.