Сьогодні ми навчимося вважати площі фігур в завданні B5 методом вузлів. Для початку введемо два визначення:
- Внутрішні вузли - це все вузли нашої координатної сітки, які опинилися всередині зафарбованою фігури;
- Граничні вузли - це такі вузли координатної сітки, які лежать на кордоні розглянутій фігури.
Давайте подивимося, як ці вузли виглядають на конкретній фігурі в завданні B5 з ЄДІ з математики:
Завдання. Знайдіть площу чотирикутника зображеного на картатій папері з розміром клітини 1 см × 1 см. Відповідь дайте у квадратних сантиметрах.
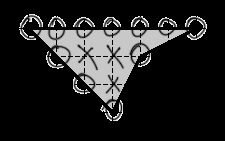
Хрестиками позначені внутрішні вузли. Очевидно, їх кількість n = 3. Кружками позначені граничні вузли. Їх загальна кількість дорівнює k = 11.
Зверніть увагу: під вузлами маються на увазі тільки ті точки, які лежать на перетині горизонтальних і вертикальних ліній нашої сітки. Іншими словами, такі дві точки не є вузлами, хоча в них межа фігури також перетинається з лініями сітки:
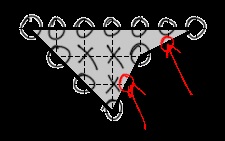
Переходимо до вирішення завдання. Для того, щоб вирішувати завдання B5 ЄДІ з математики методом вузлів, вам буде потрібно запам'ятати наступну теорему:
Нехай дана фігура з n внутрішніми вузлами і k граничними вузлами. Тоді площа цієї фігури S обчислюється за формулою:
Ось так все просто! Головне - запам'ятайте, що n - це число внутрішніх вузлів, а k - число граничних вузлів.
У нашому випадку ми вже підрахували, що n = 3, k = 11. Підставляємо отримані числа в формулу і отримуємо:
S = 3 + 0,5 · 11 - 1 = 3 + 5,5 - 1 = 7,5
Ось і все рішення! Ми отримали відповідь: площа чотирикутника дорівнює 7,5. Як бачите, завдання звелася практично до усного рахунку. Тому обов'язково візьміть даний прийом на озброєння, адже велика ймовірність того, що на цьому ЄДІ з математики вам попадеться саме таке завдання B5 - площа фігур на координатної сітки.
- Небезпечні помилки в завданнях на площі
- Метод вузлів в завданні B5
- Рішення квадратних рівнянь
- Наслідки з теореми Вієта
- Метод інтервалів: рішення найпростіших строгих нерівностей
- Завдання B5: площа кільця
- Безкоштовна підготовка до ЄДІ 7 простих, але дуже корисних уроків + домашнє завдання
