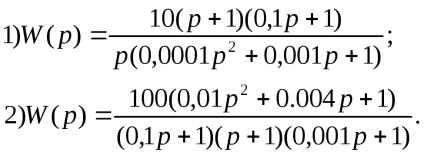
2.3. Побудова логарифмічних частотних характеристик замкнутих САУ
Для послідовного з'єднання ланок САУ, результуючі Лах і ЛФХ можуть бути отримані графічним складанням відповідних частотних характеристик ланок.
Для з'єднань типу згідно-паралельного (рис.2.6, а) або зустрічно-паралельного (рис.2.6, б) (замкнута САУ) побудова результуючих логарифмічних частотних характеристик здійснюється дещо складніше.
Якщо ланки з частотними передавальними функціями (ППФ) ісоедінени згідно-паралельно, то результуюча ППФ
,
Вираз (1 + АP e j p) являє собою частотну передавальну функцію еквівалентного послідовного ланки
Тоді вирази для ординат результуючих характеристик візьмуть вигляд:
З виразу (2.10) видно, що ординати шуканих частотних характеристик при згідно-паралельному з'єднанні ланок визначається координатами характеристик ланки з більшою на даній частоті амплітудою Аб. складеної з поправкою. яка визначається за ординатам характеристик еквівалентного послідовного ланки.
Для замкнутої САУ (рис.2.6, б) ППФ має вигляд:
,
де А2обр = 1 / А2; 2обр = - 2 - зворотні значення амплітудної і фазової характеристик ланки в зворотного зв'язку.
,
і запишемо вираження для результуючих Лах і ЛФХ:
В діапазоні частот, де А1> А2обр. здійснюється заміна A1 = AБ; 1 = б; А2обр = АМ; 2обр = М. яка також призводить до форми (2.11) для знаходження шуканих характеристик.
Таким чином, ординати шуканих частотних характеристик при зустрічно-паралельному з'єднанні ланок визначаються в більшій мірі координатами характеристик ланки з меншою на даній частоті амплітудою А i за вирахуванням поправок, що обчислюються за значенням ординат характеристик вихідних ланок.
Підкреслимо, що для ланки, що стоїть в зворотного зв'язку, необхідно зображати зворотні ЛЧХ, які можуть бути отримані з вихідних L2 () і 2 () симетричним відображенням відносно частотної осі.
На практиці використовується найпростіший спосіб наближеного побудови ЛЧХ паралельних з'єднань, заснований на апроксимованих характеристиках. Даний підхід правомірний для систем, в яких відсутні сполуки, що призводять до виникнення резонансних сплесків Лах або до появи немінімально-фазових еквівалентних ланок.
Правила побудови апроксимованих Лах паралельних з'єднань виходять з сформульованих вище правил (2.10) і (2.11) побудови точних ЛЧХ таких з'єднань в припущенні, що амплітудні поправки дорівнюють нулю.
Тоді правило для побудови наближених ЛЧХ може бути сформульовано таким чином.
Результуюча Лах паралельно з'єднаних ланок проводиться за верхнім ділянок ЛАХ складових ланок при згідно-паралельному з'єднанні і по нижніх ділянках Лах при зустрічно-паралельному з'єднанні, причому при зображенні вихідних Лах при зустрічно-паралельному з'єднанні для ланки в зворотного зв'язку зображується зворотна Лах.
Побудувати Лах для згідно-паралельного з'єднання інтегруючого ланки і апериодического першого порядку, де k1 = 100; k2 = 1000, T = 0,1c.
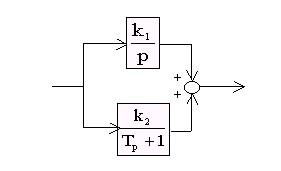
Рішення. Зобразимо Лах зазначених ланок:
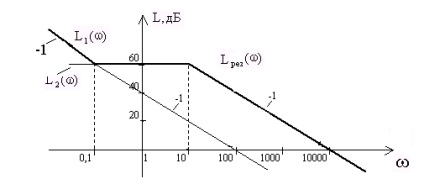
Позначимо Лах інтегруючого ланки L1 (), а Лах аперіодичної ланки L2 (). Очевидно, що в діапазоні частот 0<<0.1с выше расположена L1 (), а при >0,1 с -1 вище Лах аперіодичної ланки. Отже, результуюча Лах Lрез () при <0,1с -1 проходит по L1 (), а при 0,1с -1 – по ломаной L2 ().
Побудувати ЛЧХ для зустрічно-паралельного з'єднання ланок:
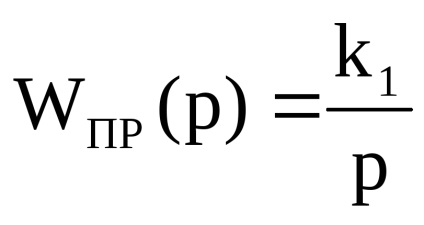
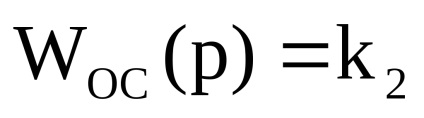
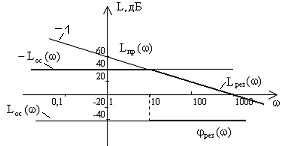
Зобразимо Лах інтегратора, що стоїть в прямому зв'язку (Lпр ()) і негативну Лах ланки в зворотного зв'язку: (-Lос ()), що представляє собою пряму, паралельну частотної осі, що проходить на рівні + 40дБ. Проводячи результуючу Лах Lрез () по нижніх ділянках, маємо Лах Lрез () = Lос () при = 10с -1 і Lрез () = Lпр () при 10с -1.