У минулій статті "Експонента і число е: гроші як приклад" ми розглянули ситуацію, коли ваші гроші ростуть експоненціально і подвоюються за певний проміжок часу.
Тепер давайте розберемося, як від цього змінюється наше розуміння суті числа е, а також що робити з системами, які ростуть експоненціально, але не подвоюються, а мають інший коефіцієнт зростання.
І що все це значить?
Число е (2.718) - це максимально можливий результат при розподілі 100% зростання протягом одного періоду часу. Звичайно, почали ми, чекаючи зростання з 1 до 2 (це і є 100% збільшення, правда?). Але з кожним крихітним кроком вперед, ми отримуємо маленькі «дивіденди», які починають самі по собі рости. Коли все сказано і зроблено, в кінці 1 періоду часу ми отримали е (2.718 ...), а не 2. Число е - це максимум, який трапляється при розбитті 100% на найдрібніші проміжки.
Так, якщо ми почнемо з 1 рубля і розкладемо безперервно 100% приросту, ми отримаємо 1е. Якщо в якості початкової суми взяти 2 рубля, в результаті отримаємо 2е. Якщо ми почнемо з 11.79 рублів, отримаємо 11.79е.
Число е - це щось на зразок межі швидкості (як "число з" - швидкість світла). Ця константа показує, як швидко можна вирости, використовуючи безперервний процес. Ви можете не завжди досягати межі швидкості, але це зручна точка порівняння: ви можете описати будь-який коефіцієнт зростання за допомогою цієї універсальної константи.
(Відступ: будьте обережні, відрізняйте поняття збільшення від поняття кінцевого результату. 1, що стає е (2.718 ...), збільшилася (коефіцієнт зростання) на 171.8%. Число е, саме по собі, є кінцевим результатом, який ви бачите після того, як весь приріст зарахований (початкова сума + приріст)).
А можуть бути інші коефіцієнти?
Гарне питання. Що якщо щорічне зростання становить 50%, а не 100%? Чи можемо ми як і раніше використовувати число е?
Давайте перевіримо. Коефіцієнт складеного зростання в 50% виглядає приблизно так:
Хм ... Що ми можемо тут зробити? Пам'ятайте, 50% - це загальний відсоток доходу, а n - це кількість періодів, на які цей відсоток поділений для нарахування (капіталізації). Якщо ми виберемо n = 50, тоді наш зростання буде поділений на 50 шматочків по 1%:
(1 + 0.50 / 50) 50 = (1 + 0.01) 50
Це, звичайно, не нескінченність, але все одно досить деталізований приклад. А тепер уявіть, що ми також поділили наш «звичайний» зростання в 100% на 1% шматочки:
число e ≈ (1 + 1.00 / 100) 100 = (1 + 0.01) 100
Ну ось, щось вже проглядається. У нашому звичному випадку у нас виходить 100 наростаючих змін, величиною 1% кожне. У випадку з 50%, у нас 50 наростаючих змін по 1% кожний.
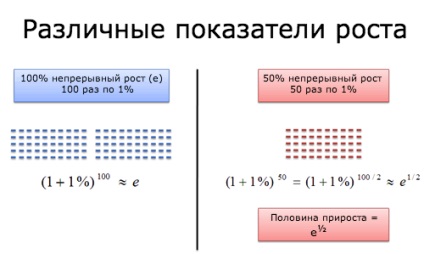
Яка різниця між двома цими числами? По суті, в випадок з 50% дорівнює половині випадку зі 100%:
(1 + 0.01) 50 = (1 + 0.01) 100/2 = ((1 + 0.01) 100) 1/2 = e 1/2
Це дуже цікаво. 50/100 = 0.5, що є показником ступеня, в яку ми зводимо е. Це загальний принцип: якби наш відсоток зростання був 300%, ми б могли розділити його на 300 шматочків по 1%. І в результаті ми б отримали результат, рівний е 3.
При тому, що зростання виглядає як просте додаток (+ 1%), потрібно пам'ятати, що насправді це множення (× 1.01). Ось чому ми використовуємо ступеня (повторюване множення) і квадратні корені (е ^ 1/2 означає «половину» кількості змін, тобто половину числа множень).
Хоча ми вибрали 1%, за коефіцієнт зростання можна було прийняти менше число (0.1%, 0.0001%, або навіть нескінченно мала кількість!). Суть в тому, що якою б коефіцієнт ми не вибрали, він буде просто означати нову ступінь для е:
зростання = e коефіцієнт
А що з приводу інших періодів часу?
Припустимо, ми виростемо на 300% протягом 2 років. Ми множимо щорічний приріст (е 3) на самого себе:
зростання = (e 3) 2 = e 6
Магія ступенів дозволяє уникати подвійного зведення. Ми просто множимо коефіцієнт на час, і зводимо число е в отриману ступінь.
По секрету: число е об'єднує приріст і час
Це дивовижно! е x може означати дві речі:
- х - кількість множень коефіцієнта зростання: 100% зростання на 3 роки складе е 3
- х - це коефіцієнт зростання сам по собі: 300% зростання за 1 рік складе е 3.
Чи не накоїть це відкриття справ? Чи не зламається наша формула, чи не настане кінець світу?
Ні, все буде в порядку. Коли ми пишемо:
змінна х являє собою комбінацію коефіцієнта зростання і часу.
Дозвольте мені пояснити. У ситуації з безперервним складовим зростанням, 10 років з 3% приростом дадуть такий же результат, як 1 рік з 30% зростанням (без подальшого зростання).
- 10 років 3% зростання означатимуть, що сума зміниться 30 разів на 1 відсоток. Ці зміни відбуваються кожні 10 років, так що кожен рік сума зростає на 3%.
- 1 період з 30% зростанням означає також 30 разів по 1%, але відбувається це все за 1 рік. Так що загальний приріст становить 30% і на цьому припиняється.
У будь-якому випадку відбувається 30 приростів по 1%. Чим вище коефіцієнт (30%), тим менше часу знадобиться, щоб дорости до того ж обсягу прибутку (1 рік). Чим коефіцієнт менше (3%), тим довше доведеться рости (10 років).
Але в обох випадках, зростання складе е 0.30 = 1.35 в результаті. Через брак терпіння ми вважаємо за краще більш високий і швидкий ріст повільного і тривалого, але число е показує, що ефект однаковий в обох випадках.
Ось така у нас виходить загальна формула:
зростання = e x = e приріст × час
Якщо за період В ми отримаємо приріст П, наш загальний складовою зростання буде дорівнює е пв. Між іншим, це також працює для негативних і дрібних приростів.
У наступній статті ми розглянемо експоненціальне зростання і число е на реальних прикладах: зростання кристалів, максимальна банківська ставка, швидкість радіоактивного розпаду.