Зірчастий багатокутник - багатокутник. вершини якого розташовані як у деякого правильного багатокутника і сторони якого перетинаються між собою. Існує безліч правильних зірчастих многокутників (або просто зірок), серед них пентаграма. дві септаграмми, октаграма. декаграмма, додекаграмма. Зірчасті багатокутники можна отримати, продовжуючи боку правильного багатокутника після їх перетину в його вершинах до їх наступного іншого попарного перетину в точках, які і є вершинами зірчастого багатокутника. Отриманий зірчастий багатокутник буде зірчастої формою правильного багатокутника, з якого він отриманий. Вершинами зірчастого багатокутника будуть вважатися тільки точки, в яких сходяться боку цього багатокутника, але не точки перетину цих сторін; Зірчаста форма даного багатокутника має стільки ж вершин, скільки він сам. Вказану операцію неможливо виконати з правильним трикутником і квадратом, так як після продовження їхнього боку більш не перетинаються; зірчасті форми мають тільки правильні багатокутники починаючи з п'ятикутника. Зірчастої формою п'ятикутника (пентагона) є пентаграма.
Зірки можуть бути нераспадающіхся єдиними багатокутниками, яка є сполуками інших правильних або зірчастих многокутників (як у випадку з пентаграммой), а можуть бути такими сполуками, прикладом чого служить Зірчаста форма шестикутника - гексаграмма. або «Зірка Давида», що є з'єднанням двох трикутників.
У правильного багатокутника може бути кілька зірчастих форм, кількість яких залежить від того, скільки разів його боку перетинаються між собою після їх продовження, прикладом чого є семикутник, має 2 звёзчатие форми (два види семикутної зірки).
Кількість вершин правильного багатокутника
Кількість зірчастих форм правильного багатокутника
Кількість нераспадающіхся (зв'язкових) зоряних багатокутників серед зірчастих форм
Кількість вершин правильного багатокутника, розташованих між двома вершинами зоряного багатокутника
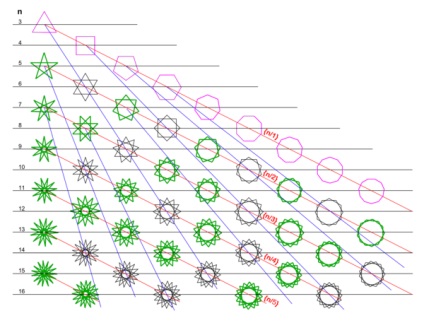
Двовимірне дискретне безліч зірок.
Пурпурні - опуклі багатокутники.
Зелені - зв'язкові зірки (де n і m взаємно прості числа).
Чорні - НЕ зв'язкові зірки (де n і Mне взаємно прості числа).
Сині прямі з'єднують багатокутник (опуклий або зв'язну зірку) зі всіма не зв'язковими зірками, які є сполуками (після повороту) різної кількості однакових багатокутників, таких же як цей
Для поліпшення цієї статті бажано.
Дивитися що таке "Зірчастий багатокутник" в інших словниках:
Зірчастий багатогранник - Зірчастий багатогранник це правильний неопуклих багатогранник. Багатогранники з за їх незвичайних властивостей симетрії досліджуються з найдавніших часів. Також форми багатогранників широко використовуються в декоративному мистецтві ... Вікіпедія
Трикутник Рело - Побудова трикутника Рело Трикутник Рело [* 1] предста ... Вікіпедія
Зоряна область - не опуклі зоряна область щодо точки ... Вікіпедія
Зоряна область - не опуклі зоряна область щодо точки x0 НЕ зоряна область Зоряна область, щодо фіксованої точки O область D евклідового простору, така, що відрізок, що з'єднує будь-яку точку області ... Вікіпедія
Октаграма - октаграма восьмипроменева зірка, крестострел. Будучи намальована вписаною в коло, уособлює порядок, творення. Без кола є символом хаосу (суть хаосу в зворотної функції розкладання щодо гармонійно сформованих ... Вікіпедія
Гексаграмма (символ) - Цей термін має також інші значення див. Гексаграмма. Правильна гексаграма ... Вікіпедія
Піраміда (геометрія) - Цей термін має також інші значення див. Пірамідацу (значення). Достовірність цього розділу статті поставлена під сумнів. Необхідно перевірити точність фактів, викладених в цьому розділі. На сторінці обcужденія можуть бути пояснення ... Вікіпедія