ВИЗНАЧЕННЯ прогину Косом ВИГИНІ
Мета роботи - ознайомлення з косим вигином консольного бру-са і порівняння досвідчених значень прогину з теоретичним.
Якщо площину дії згинального моменту, що виникає в поперечному перерізі бруса, не збігається ні з однією з його головних осей, то такий вигин називається косим.
При плоскому косому вигині все навантаження розташовані в одній площині. В цьому випадку пружна лінія бруса - плоска крива, але на відміну від прямого вигину площину, в якій вона розташована, не збігається з площиною дії навантажень (рис.1).
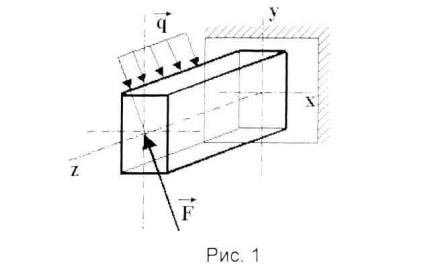
При просторовому косому вигині навантаження, що викликають вигин, розташовані в різних поздовжніх площинах бруса (рис.2). Пружна лінія в цьому випадку - просторова крива.
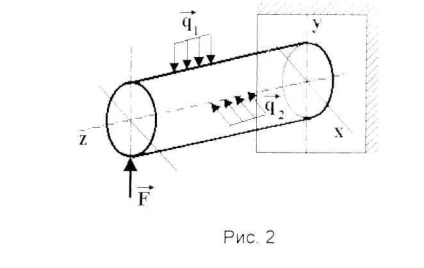
При поперечному косому вигині (як плоскому, так і достатньо міс-венном) в поперечному перерізі бруса виникають чотири внутрішніх силових фактори поперечні сили Qx. Qy і згинальних моментів Мх. Му.
Розглянемо плоский косою вигин на прикладі бруса, навантажений-ного однією силою, яка додається в площині торцевого перетину таким чином, що її лінія дії становить кут # 946; з головною центральною віссю OY (рис.3).
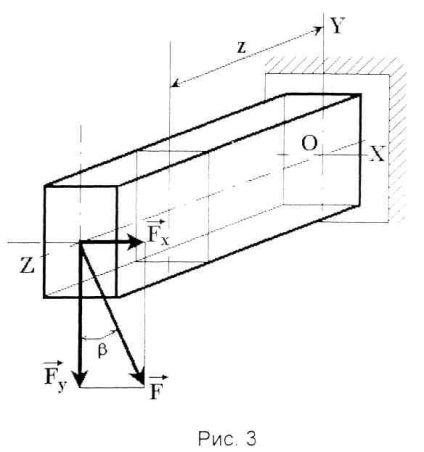
Розкладемо силу на складові = + y по головних осях поперечного перерізу ОХ і OY. Кожна з цих складових викликає прямий вигин бруса в одній з головних площин:
сила Fy = F * cos # 946; - в площині ZOY
і сила Fx = F * sin # 946; - в площині ZOX.
Таким чином, косою вигин можна розглядати як сукупність-ність двох прямих вигинів у взаємно перпендикулярних площинах ZOY і ZOX.
Для бруса, жорстко защемленого одним кінцем і навантаженого силою на вільному кінці, вираз для прогинів торцевого січі-ня має наступний вигляд:
де fx. fy - прямі прогини в площинах ZOX і ZOY відповідно;
Е-модуль пружності матеріалу бруса;
Jx. Jy - моменти інерції перерізу щодо осей ОХ і OY відповідно;
F- сила, що діє на брус;
# 946; - кут між лінією дії сили F і головною віссю перерізу OY.
Повний прогин вільного кінця (рис.4)
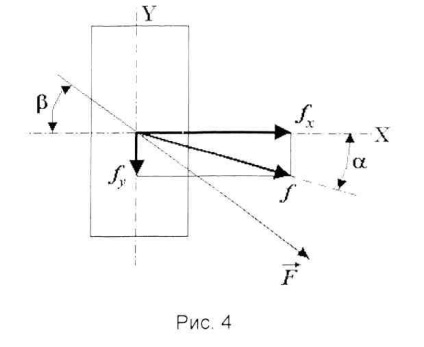
Визначимо напрямок повного прогину за формулою:
де # 945; - кут між напрямком повного прогину і головною віссю OY.
Якщо JХ = Jy нульова лінія перпендикулярна силової лінії. В цьому випадку вигин буде тільки прямим. Це можливо в разі, коли будь-яка центральна вісь перетину - головна вісь. Таким чином, для перетинів типу кола, квадрата і т.п. у яких всі центральні осі - головні, косою вигин неможливий.
Устаткування і матеріали:
1. Установка ТМТ - 13;
2. Індикатори годинникового типу ИЧ - 10;
3. Вантажі підвісні.
Установка (рис.5) виконана в настільному виконанні і з-стоїть зі звареного підстави 1, на якому справа закріплена стійка 2 у вигляді усіченої піраміди, а зліва циліндрична стійка 3.
При виконанні лабораторної роботи на установці использу-ються три балки. Одна з них має прямокутний поперечний січі-ня, інша - равнобокой куточок, третя - кругла. Балка правим кінцем закріплюється на корпусі 5, які мають кутову шкалу для ус-тановки кута повороту балки, і фіксується кришкою 6. На лівому кінці контрольної балки встановлена на шарикопідшипнику сережка 7, за яку зачіпається підвіс 8 з вантажами. На стійці 3 закріплений кронштейн з двома індикаторними головками 9,
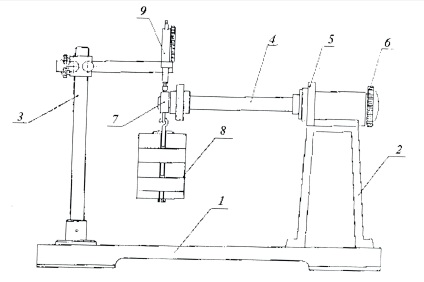
Ціна одного ділення індикатора годинного типу - 0,01 мм. Один оборот великої стрілки відповідає вертикальному пере-міщення штока індикатора на 1 мм. Повний робочий хід штока - 10 мм.
До роботи з вказаною установкою допускаються особи, ознайомлені з її пристроєм, принципом дії і порядком проведення роботи.
Порядок виконання роботи:
2. Звільнити фіксуючу кришку 6. Встановити контрольну балку в корпус 5. Зафіксувати балку під заданим кутом поворотів-та балки. Переконатися в стійкості установки.
3. Переконатися, що запас ходу штоків індикаторних головок 9 в ниж-ньому напрямку становить не менше 10 мм, при необхідності перевстановити головку.
4. Провести юстировку показань індикаторних головок при за-кріпленні контрольної балки без навантаження вантажами.
5. Отримати у викладача завдання на виконання роботи.
6. Навантажити балку послідовно однаковими вантажами.
7. За допомогою індикаторних головок 9 зробити виміри гори-зонтальним fгор і вертикальної fвepm складових прогину балки виникають під дією вантажів.
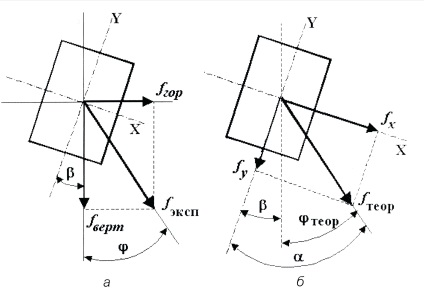
8. Визначити тангенс кута нахилу лінії прогину до вертикалі # 966; (Рис.6, а) за формулою
9. Визначити величину повного прогину fексп (рис.6, а) за формулою
Відповідно до того, що балка навантажується в кілька етапів, по-лучім кілька значень fексп і # 966 ;. З цих значень слід взяти середнє арифметичне значення f0 і # 966; 0.
10. Розрахувати теоретичні величини прямих вигинів fx і fy (рис. 6, б) за формулами (1) і (2).
11. Визначити теоретичну величину повного прогину по фор-мулі (3).
12. Визначити тангенс кута нахилу лінії прогину до осі OY (# 945;) за формулою (4).
13.Определіть теоретичне значення кута нахилу лінії про- згину до вертикалі # 966; теор (рис.6, б) за формулою
14.Сравніть результати, отримані експериментальним путем0. # 966; 0) з теоретичними (fтеор, # 966; теор).
1. У чому полягає явище косого згину? За яких умов виникає косою вигин?
2. Як обчислюються складові прогину по головних осях?
3. Як обчислити повний прогин і визначити його напрямок?
4. Як визначити напрям нейтральної лінії при косому вигині?
5. Які прилади використовуються для експериментального визначення прогину? Що називають ціною поділки шкали приладу?
6. У яких випадках косою вигин неможливий?
7. Які осі називають головними? Для яких перетинів положення головних осей очевидно? Наведіть приклади.