З визначення інтегруючого множника маємо
або ж, ділячи обидві частини рівності (10.20) на,
Ми отримали у вигляді (10.20) або (10.20 ') рівняння в приватних похідних для визначення невідомої функції. Завдання інтегрування такого рівняння в загальному випадку не простіше, ніж завдання вирішення рівняння (10.6). Звичайно, нам досить знати тільки одне приватне рішення рівняння (10.20) іноді по якимось особливостям рівняння (10.20), вдається знайти таке приватне рішення, і тоді інтеграція рівняння (10.6) зводиться до квадратурі.
Розглянемо, наприклад, випадок, коли існує інтегруючий множник, що є функцією одного тільки х.
У цьому випадку = 0 і рівняння (10.20 ') звертається в таке
Ясно, що для існування інтегруючого множника, що не залежить від у необхідно і достатньо, щоб права частина була функцією одного х, в такому випадку знайдеться квадратурою:
Приклад 10.6: (2ху + х 2 у +) d х + (х 2 + у 2) dу = 0
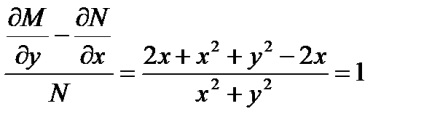
Отже, = 1, = х, = е х
є рівняння в повних диференціалах. Інтегруємо його,
Для знаходження (у) обчислимо і прирівняємо його N
і загальний інтеграл нашого рівняння є
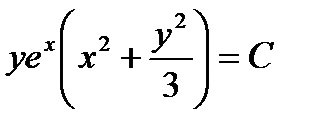
Розглянемо окремий випадок інтегруючого множника, що залежить тільки від x, коли N = 1 в цьому випадку рівняння має вигляд
Рівняння (10.21) набуде вигляду
з умовою. що є функція одного х.
В такому випадку f (х, у) має вигляд
тобто рівняння, написане у вигляді (10.22) і допускає інтегруючий множник, що залежить тільки від х є рівняння лінійне.
З рівняння (10.21) маємо
Переходячи до позначень лекції 9 для лінійного рівняння, приходимо до висновку.
Лінійне рівняння має інтегруючий множник
Прімер10.7: Рівняння має інтегруючий
множник. множачи на нього обидві частини рівняння, маємо
де ліва частина є повний диференціал, інтегруючи знаходимо