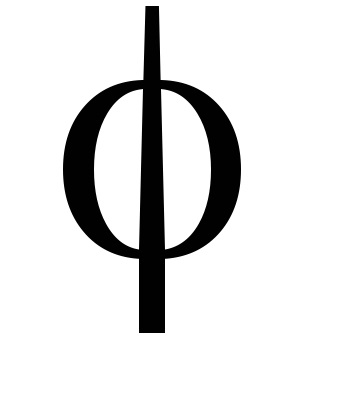
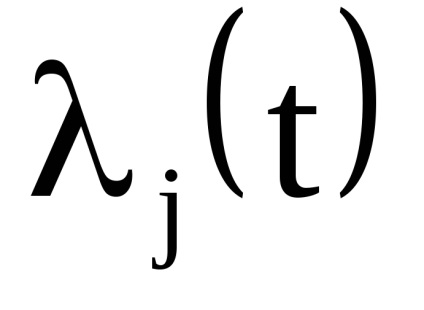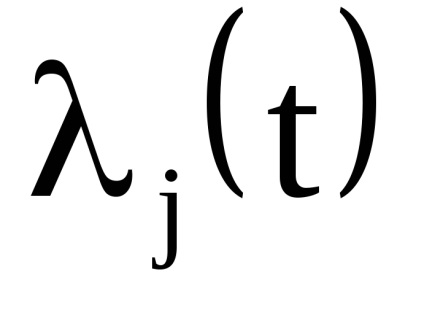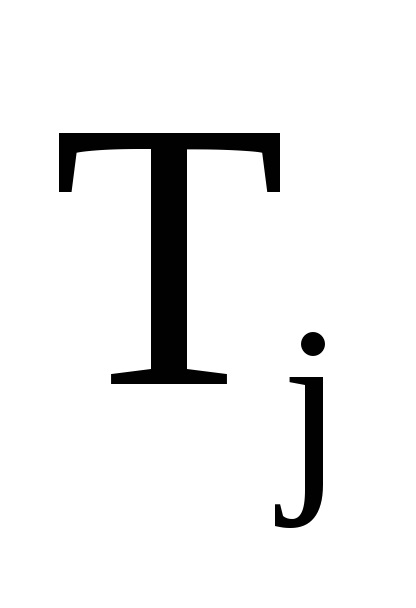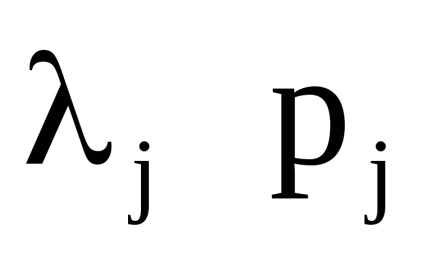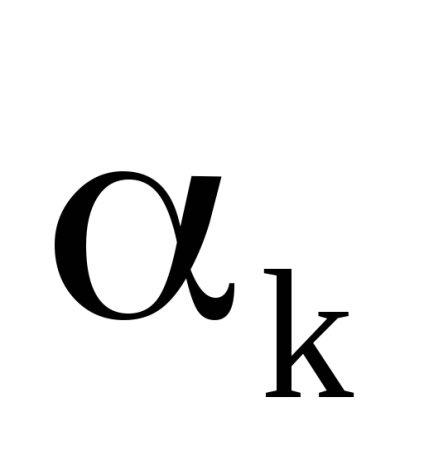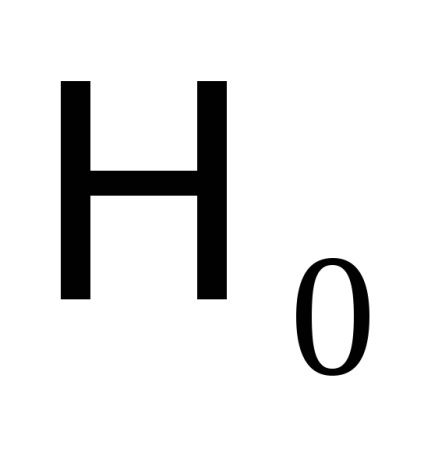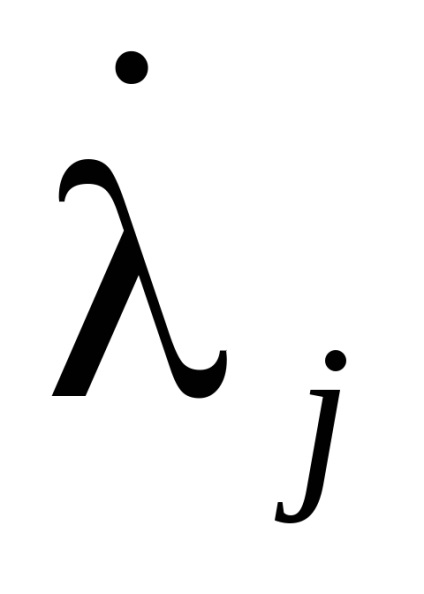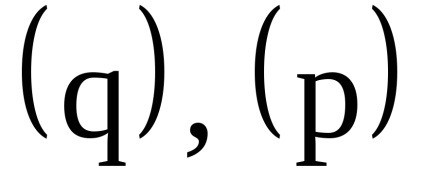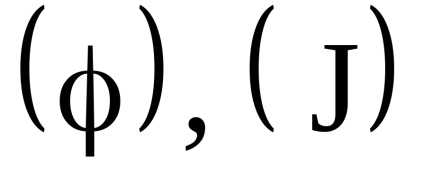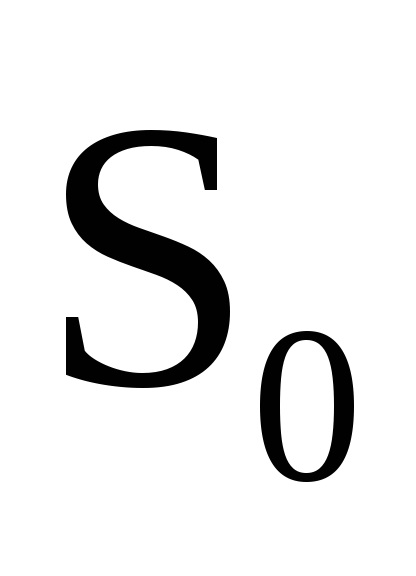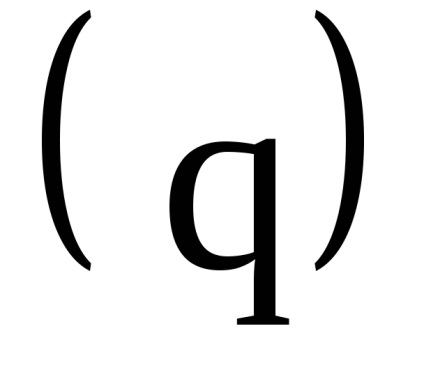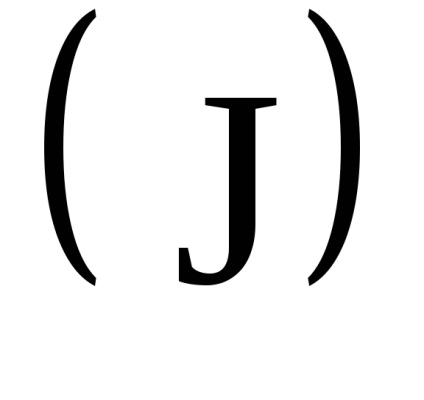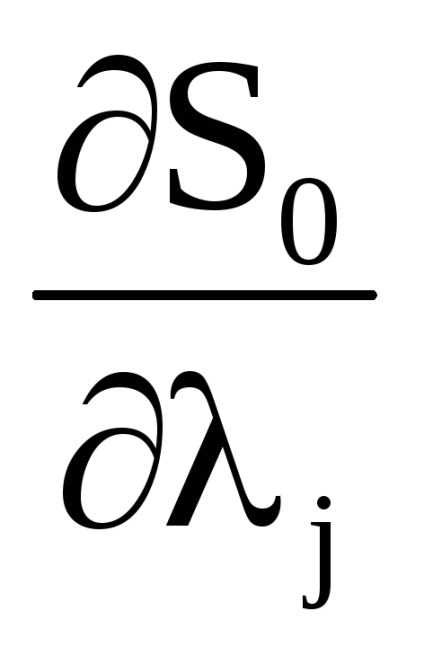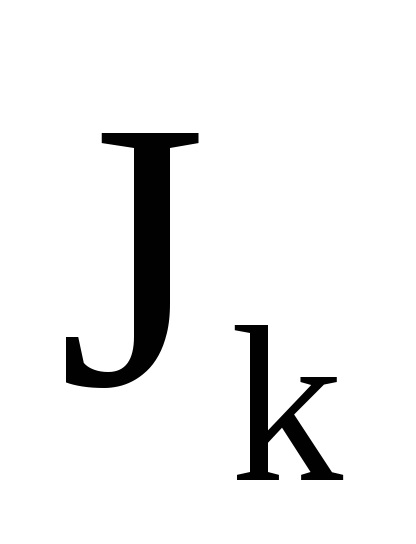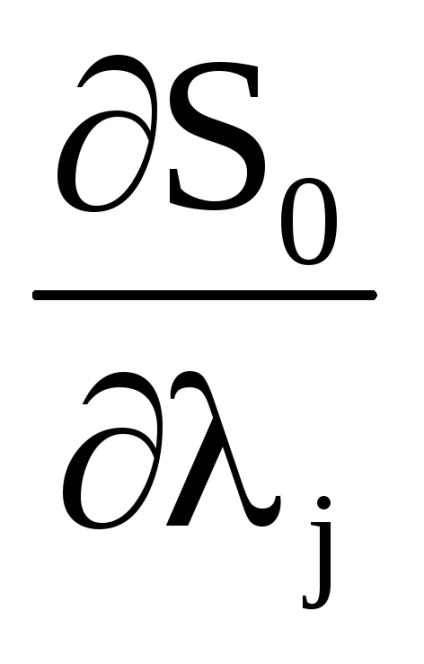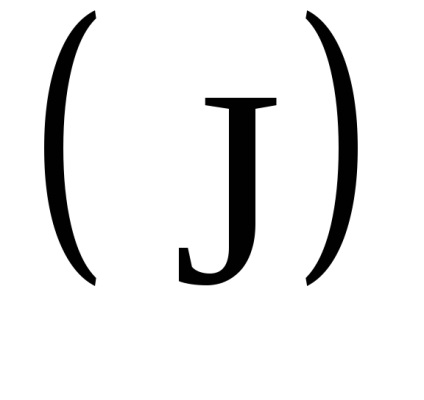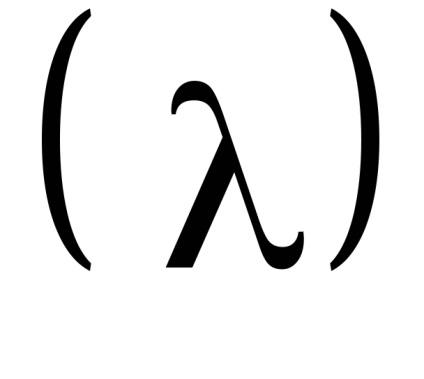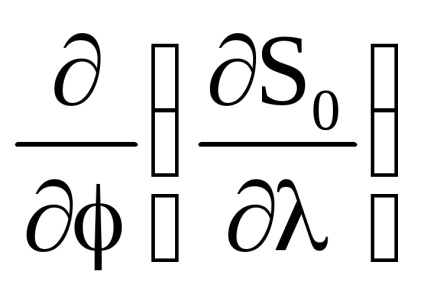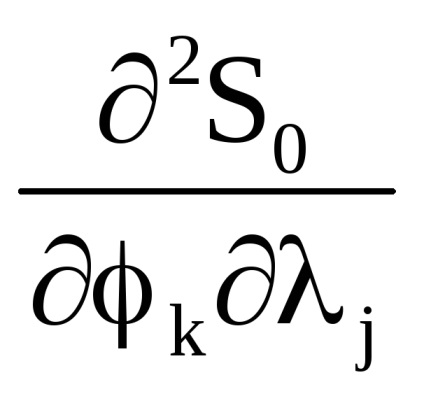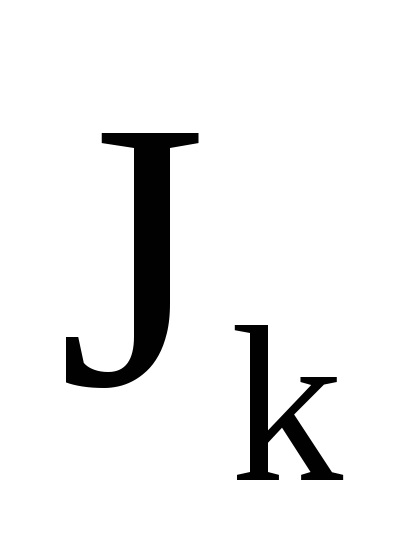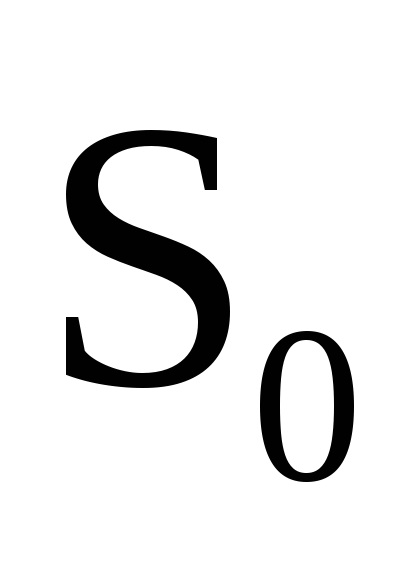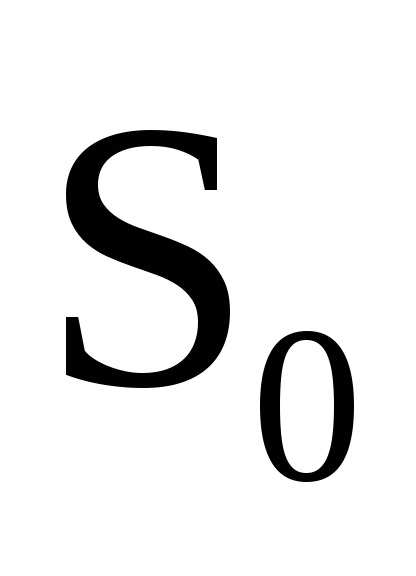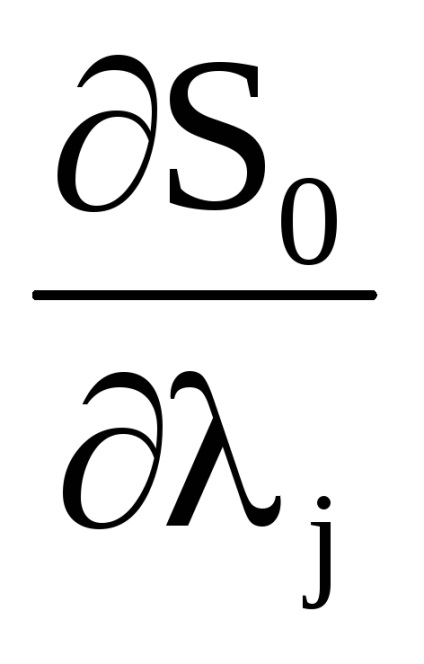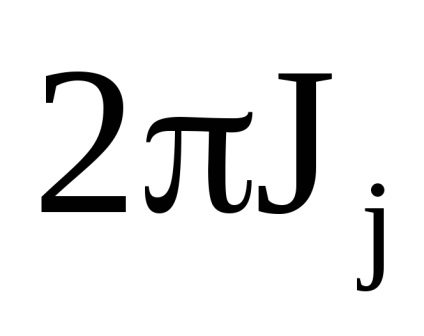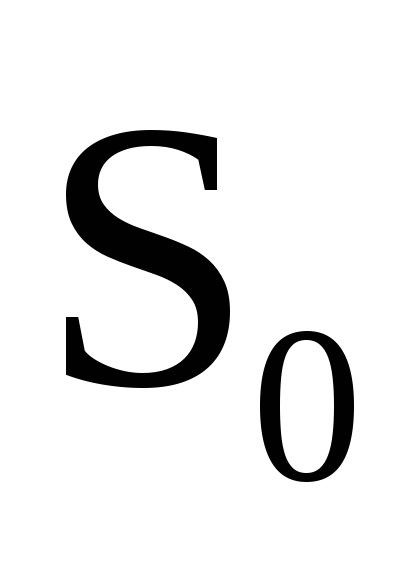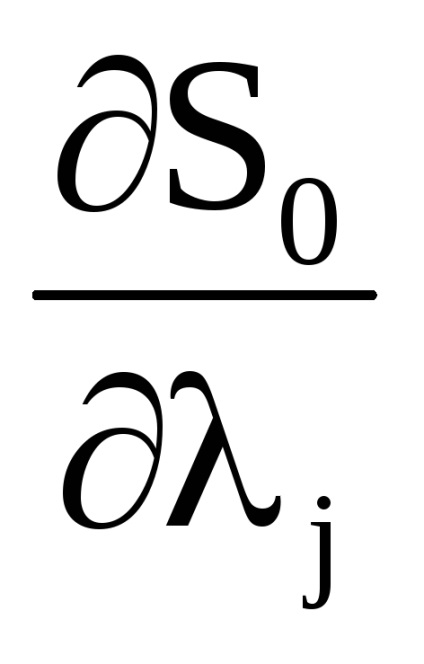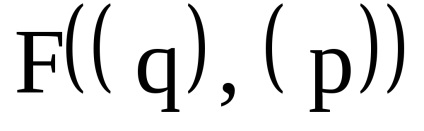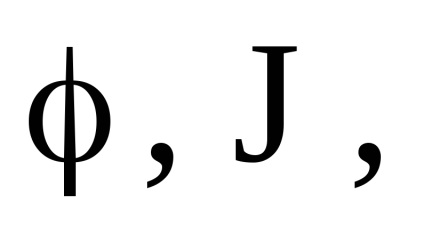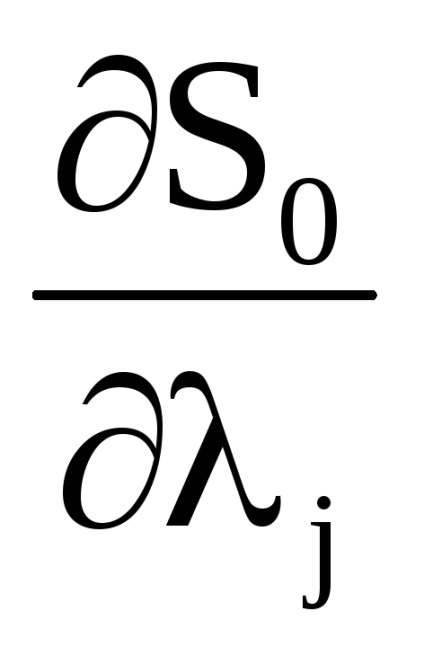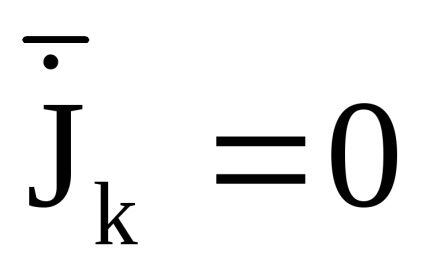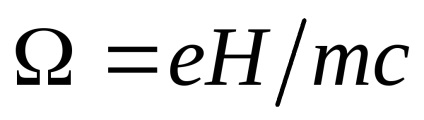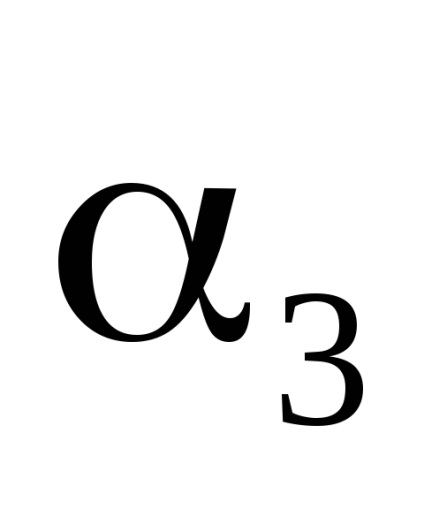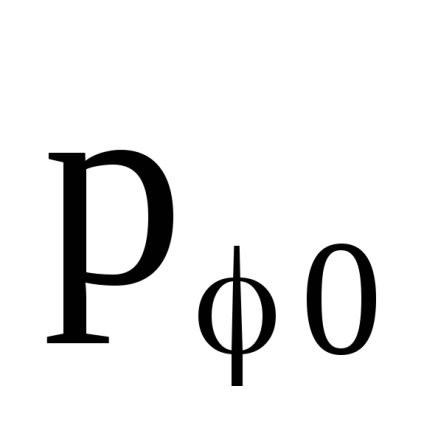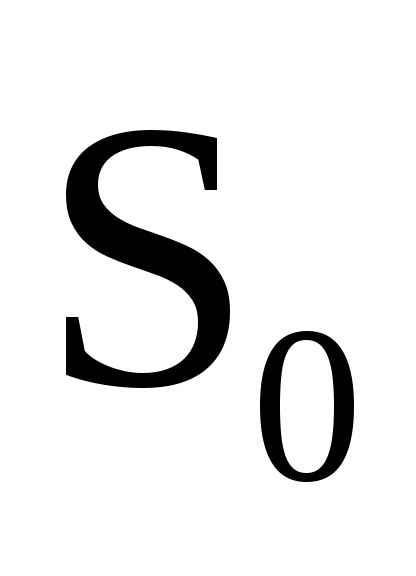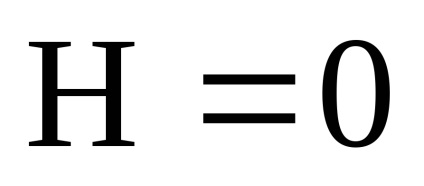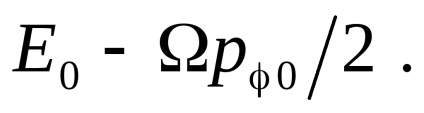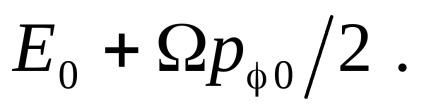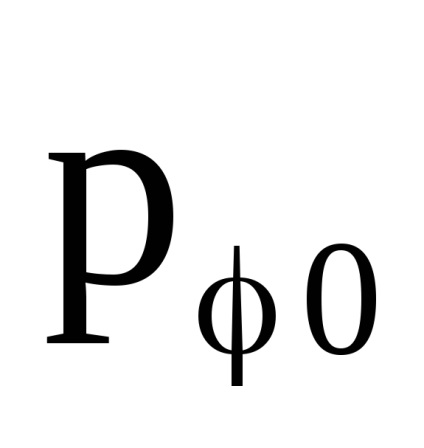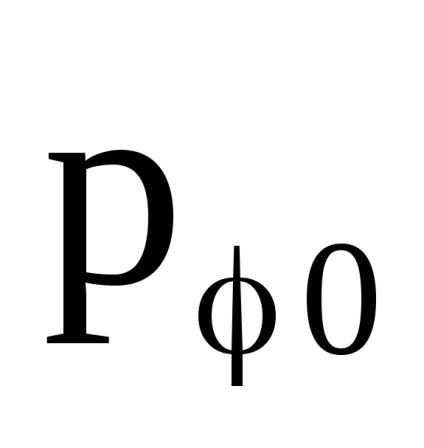Важливою властивістю змінних дії є властивість адіабатичній інваріантності, яке полягає в тому, що змінні дії зберігають свої постійні значення і в тих випадках, коли гамільтоніан системи залежить від часу через деякі параметри
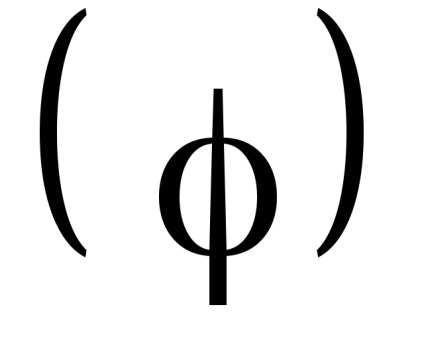
, які, як кажуть, адиабатически змінюються з часом, т. е. дуже повільно. Під повільними маються на увазі такі зміни, при яких
мало змінюються за відрізки часу, рівні по порядку величини періодів
, т. е.
Ясно, що такі механічні системи не є строго ізольованими. Покажемо, що змінні дії в таких системах є адіабатичними інваріантами.
Розглянемо систему, збігається в кожен момент часу з вивченої вище консервативною системою, яка допускає повне розділення змінних. Припускаємо також, що рух системи ФІНІТНОГО. Гамільтоніан такої системи явно залежить від параметрів
, які задовольняють умовам (61.11); його можна представити у вигляді
при постійному
є періодичними функціями відповідних координат
;
в даному випадку є періодичними функціями часу.
якщо параметри
змінюються з часом повільно, то, незважаючи на те що система, описувана гамильтонианом (62.11) не консервативною, рішення рівняння Гамільтона-Якобі можна шукати у вигляді, близькому до (24.11):
де, однак, параметри
, а тому і величини
і
повільно змінюються з часом. Підставляючи (63.11) в рівняння Гамільтона-Якобі і нехтуючи в ньому членами, пропорційними
, отримаємо рівняння «нульового наближення»
В силу (61.11) це рівняння можна вирішувати, вважаючи все
постійними, і лише в побудованих рішеннях вважати їх заданими функціями часу. Тому все формули, отримані вище для консервативної системи залишаються справедливими, але в усі співвідношення тепер увійдуть залежать від часу параметри
.
Виробляє функція канонічного перетворення від змінних
до змінних
визначається функцією
, яка тепер, однак, буде залежати і від
:
Зауважимо, що
також залежать від
.
Напишемо формули канонічного перетворення, що генерується функцією (65.11):
Нові рівняння руху мають вигляд
У всіх формулах диференціювання по
повинно проводитися при постійних
і
; після диференціювання в формулах (69.11), (70.11) виконується підстановка (67.11) і похідні
виражаються через.
Для доказу властивості адіабатичній інваріантності змінних
усереднити рівняння (70.11) по інтервалу часу, малому в порівнянні з часом помітного зміни параметрів
і досить великим у порівнянні з періодами системи. При такому виборі інтервалу часу величини
(В силу повільного зміни
) Можна виносити з-під знака середнього. отже,
Покажемо тепер, що похідні
є однозначними періодичними функціями
. Якщо це так, то тоді їх можна буде розкласти в ряди Фур'є, коефіцієнти яких будуть залежати від
і
. У свою чергу ряди Фур'є для похідних
не міститимуть постійних членів, і тому при усередненні по досить великим інтервалу часу все похідні
звернуться в нуль і адіабатична инвариантность всіх
буде доведена.
Зауважимо, що
- неоднозначна функція координат
, так як згідно (66.11) її можна представити у вигляді
За повний період зміни координати
(При інших фіксованих)
бере зріст
функції
- однозначні функції координат, так як при диференціюванні по
добавки, кратні
, які призводять до неоднозначності
, зникнуть. Так як
- однозначні функції координат
, то вони є періодичними функціями кутових змінних
; ці функції не будуть змінювати свої значення при зміні
на
(При заданих значеннях
). Іншими словами, будь-яка однозначна функція
, виражена через канонічні змінні
є періодичною функцією кожної
з періодом, рівним
. Отже все
є однозначними періодичними функціями
. Вище ми показали, що в цьому випадку все
і, отже, все
Властивість адіабатичній інваріантності всіх змінних дії доведено.
Приклад. Як зміниться енергія зарядженої частинки е маси т в центральному полеU (r) при повільному включенні слабкого однорідного магнітного поля напруженості Н?
Запишемо функцію Гамільтона заряду в сферичної системі координат (вісь Oz декартової системи координат паралельна H):
тут
- швидкість світла. За умовою завдання магнітне поле слабке, тому останнім членом (квадратичним по H) нехтуємо.
Рівняння Гамільтона-Якобі з урахуванням цього набуває вигляду
де
- енергія частинки,
-циклотронна частота.
Рішення шукаємо у вигляді
Тут в якості постійної
ми вибрали
. підставляючи
в (74.11), одержуємо
Рівняння (75.11) визначає функцію яка потрібна для обчислення змінної дії
:
очевидно,
збігатиметься з
, обчисленим для випадку
, якщо в останньому виразі замість
підставити комбінацію
Значить, величина
залишається постійною при повільному включенні однорідного магнітного поля. Крім неї постійної буде величина
- компонента узагальненого імпульсу заряду. За фізичним змістом
- зберігається проекція моменту імпульсу заряду на вектор H.
Схожі статті