77. Нам вже доводилося будувати чотирикутники (п. 50). Тепер розширимо це побудова. Нехай дано 4 точки: A, B, C і D [чер. 84 (I)]; побудуємо всілякі прямі з'єднують попарно ці 4 точки - ми вважаємо, що ніякі 3 з даних точок не розташовані на одній прямій. Таких прямих можна всього побудувати 6 (з кожної точки до трьом іншим йдуть 3 прямих, так як точок 4, то найбільше прямих 3 * 4 = 12, але кожна пряма тут вважалася два рази, напр. Пряма AC: один раз ми її вважали що йде від A до C і іншим разом - від C до A, тому різних прямих повинно бути (4 * 3) / 2 = 6). Отримана фігура складається з 4 точок і 6 з'єднують їх попарно прямих, - вона називається повним чотирикутником. Кожна з даних чотирьох точок називається його вершиною. а кожна входить до його складу пряма - його стороною. у повного 4-кутника 4 вершини і 6 сторін.
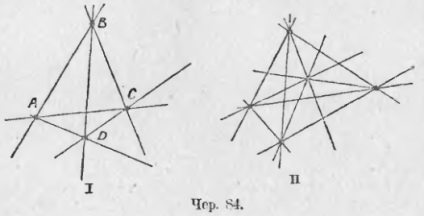
Якщо ми візьмемо 5 точок (чер. 84 - II), щоб ніякі 3 з них не лежали на одній прямій, і з'єднаємо їх попарно прямими, то отримаємо повний 5-кутник; у нього 5 вершин і 10 сторін. У повного 6-кутника 6 вершин і 15 сторін і т. Д.
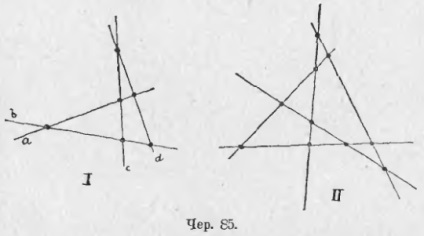
Навпаки, можна побудувати 4 прямих a, b, c і d (чер. 85 - I) так, щоб ніякі три з них не проходили через одну точку, і знайти їх точки перетину. Припустимо, що серед прямих a, b, c і d немає жодної пари паралельних; тоді кожна пряма з трьома іншими перетинається в трьох точках, а всього точок перетину 3 * 4 = 12, але тут кожна точка вважалася 2 рази: один раз, напр. від перетину прямої a з прямою b, а іншим разом від перетину прямої b з прямою a; тому число різних точок перетину має бути 4 * 3/2 = 6. Отримана фігура, що складається з 4 прямих і 6 точок їх перетину, називається повним четирехсторонников; кожна пряма називається його стороною і кожна точка - його вершиною. У четирехсторонников 4 сторони і 6 вершин. Якщо таке ж побудова виконати з 5 прямими, то отримаємо повний пятістороннік (чер. 85 - II). У нього, якщо покладемо, що серед 5 прямих немає жодної пари паралельних, 5 сторін і 10 вершин. У повного шестісторонніка (з тою ж застереженням щодо прямих) 6 сторін і 15 вершин і т. Д.
78. Візьмемо знову кілька точок і з'єднаємо їх попарно прямими, але не кожну з кожної, а, намітивши попередньо їх порядок, кожну з подальшою (останню знову з першої). Побудована таким чином фігура зветься: простий багатокутник - на чер. 86 дано зображення простих 5-кутника і 6-кутника.
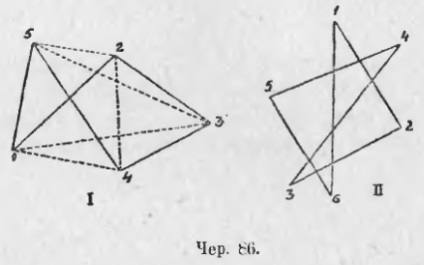
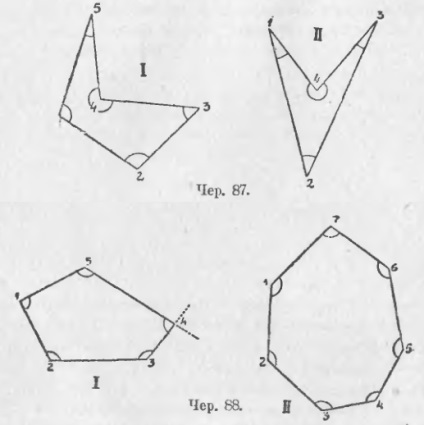
Порядок взятих точок на кресленні позначений цифрами: тут треба, щоб три сусідніх точки не лежали на одній прямій. Кожна точка, що входить до складу простого багатокутника, називається його вершиною і кожна пряма - його стороною (ми можемо тут, як це було і в трикутнику, розуміти під цим ім'ям лише відрізок прямої, що з'єднує дві сусідні вершини багатокутника). Не важко побачити, що в простому багатокутнику стільки ж сторін, як і вершин. Якщо з'єднати прямою дві несоседних вершини, то отримана пряма (або її відрізок, укладений між взятими вершинами) називається діагоналлю цього багатокутника. На чер. 86 (I) побудовано пунктиром 5 діагоналей простого п'ятикутника. У простому шестикутнику можна побудувати 9 діагоналей (на чер. 86 - II вони не побудовані). Так як у простого багатокутника сторін стільки ж, скільки і вершин, то їх можна ще називати простими многостороннікамі (простий пятістороннік і т. П.). На чер. 87 і 88 дано ще різні види простих багатокутників.
79. У курсі елементарної геометрії розглядаються тільки прості багатокутники, а тому їх часто називають одним словом багатокутники. При побудові простих багатокутників можуть бути два випадки: 1) сторони багатокутника, розуміючи під цим ім'ям відрізки прямих між двома вершинами, перетинають один одного (див. Чер. 86) і 2) не перетинають один одного (чер. 87 і 88). Між цими двома випадками суттєва різниця. У той час, як в другому випадку ми бачимо, що багатокутник виділяє з площини її певну частину, яка називається площею цього багатокутника, в першому випадку ми бачимо, що там виділяється кілька частин - особливо це помітно на чер. 86, II, - причому можна виділити навіть іноді такі дві частини, що одна з них почасти накладена на іншу; тут, отже, ми не бачимо відразу площа. що обмежується цим многоугольником. Тому ми будемо називати багатокутники, які підходять під другий випадок (чер. 87 і 88), що мають площу. і багатокутники, які підходять під перший випадок (чер. 86) - не мають площі (їх ще називають зірчастими).
Слід зауважити, що, зробивши кілька умов, що дозволяють частини площині вважати те позитивними, то негативними, можна вважати, що всякий багатокутник має площу. Питання про площі зірчастих многокутників не входить в курс елементарної геометрії.
Часто ще розглядають так званий периметр багатокутника; цим ім'ям називають суму всіх сторін багатокутника.
80. У елементарної геометрії майже виключно розглядаються багатокутники, які мають площу. При кожній вершині такого багатокутника виходять кути, по 4 кута при кожній, якщо під сторонами багатокутника розуміти нескінченні прямі (напр. См. Кути при вершині 4 п'ятикутника I чер. 88). Один з цих кутів, внутрішня область якого захоплює площа багатокутника, називається внутрішнім; при кожній вершині багатокутника виходить по одному внутрішньому куті (на чер. 87 і 88 внутрішні кути відзначені дугами).
Тут знову виникає поділ багатокутників, що мають площу, на два класи: 1) кожен внутрішній кут багатокутника менше випрямленої кута, - такі багатокутники називаються опуклими (чер. 88); 2) може статися, що один або кілька внутрішніх кутів більше випрямленої (на чер. 87 кути при вершинах 4 в обох багатокутниках), - такі багатокутники називаються неопуклого.
Кутника можна має властивість, що всі його вершини розташовані по одну сторону від кожної його боку (розуміючи під цим ім'ям нескінченну пряму). Неопуклих багатокутник цією властивістю не володіє.
Надалі нам доведеться мати справу, головним чином, з опуклими багатокутниками.
81. Першою нашою задачею про багатокутники є знаходження суми внутрішніх кутів багатокутника.
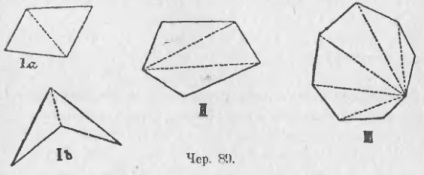
Якщо ми візьмемо будь-якої чотирикутник, що має площу [чер. 89, I (a) або I (b)], і побудуємо одну з його діагоналей - в разі I (a) байдуже яку, а в разі I (b), ту, яка розташована на площі цього 4-кутника (всередині його ), то отримаємо 2 трикутника. Сума внутрішніх кутів кожного трикутника 2d, отже, сума внутрішніх кутів 4-кутника = 2d * 2 = 4d. Якщо візьмемо будь-якої 5-кутник і побудуємо дві діагоналі, що йдуть з однієї його вершини (чер. 89, II), то отримаємо 3 трикутника; так як сума внутрішніх кутів трикутника = 2d, то сума внутрішніх кутів 5-кутника = 2d * 3 = 6d; також для 6-кутника отримаємо 4 трикутника і, отже, сума його внутрішніх кутів = 2d * 4 = 8d і т. д. Якщо візьмемо, напр. 11-кутник, то після побудови діагоналей отримаємо 9 трикутників. Сума внутрішніх кутів 11-кутника = 2d * 9 = 18d. Взагалі, якщо візьмемо n-кутник, то після побудови діагоналей з однієї його вершини отримаємо (n - 2) трикутників і, отже, сума внутрішніх кутів цього багатокутника виразиться формулою:
де n висловлює число сторін або вершин цього багатокутника.
82. Другим питанням буде питання про суму зовнішніх кутів багатокутника. Під назвою «зовнішній кут» можна розуміти, як це ми вже і робили для трикутника, кут, складений продовженням одного боку багатокутника зі наступну стороною (∠I, ∠II і т. Д. На чер. 90). Станом йти по сторонам цього багатокутника, який вважатимемо опуклим, напр. у напрямку, зазначеному стрілками, і кожну з сторін продовжувати в тому ж напрямку. Тоді отримаємо ряд зовнішніх кутів: ∠I, ∠II і т. Д. Розглянемо спочатку одну пару кутів: внутрішній і зовнішній при загальній вершині, напр. ∠1 і ∠I; тоді ми бачимо, що сума їх є випрямленний кут, т. е.
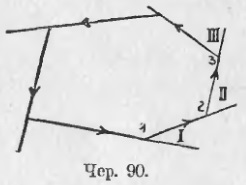
Також знайдемо при іншій вершині: ∠2 + ∠II = 2d і т. Д. Якщо покладемо, що всього вершин в багатокутнику було n, таких пар кутів також n, і отже:
(Сума внутрішніх кутів) + (сума зовнішніх кутів) = 2d * n
Але ми знаємо, що
сума внутрішніх кутів = 2d (n - 2).
Сума зовнішніх кутів = 2dn - 2d (n - 2) = 2dn - 2dn + 4d = 4d
т. е. сума зовнішніх кутів опуклого багатокутника не залежить від числа сторін (або вершин) цього багатокутника і завжди дорівнює 4d.
83. Додавання. Можна назва «зовнішній кут» розуміти і в іншому сенсі. Нехай маємо будь-якої багатокутник (чер. 91), що має площу, хоча б і не опуклий. Тоді під зовнішнім кутом можна розуміти кут, складений сторонами багатокутника, а не їх продовженнями, як і внутрішній кут, напр. ∠BAC, але за внутрішню його область прийняти ту частину площині, що виділяється сторонами цього кута, яка не містить в себе площі цього багатокутника. Внутрішня область кожного з цих кутів відзначена на кресленні дугою. Тоді кожен такий кут, разом з відповідним йому внутрішнім кутом, становить 2 випрямлених кута або 4d, напр. внутрішній ∠BAC + зовнішній ∠BAC = 4d.
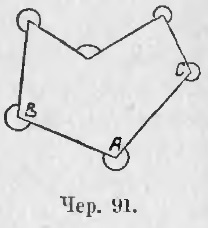
Якщо сторін у багатокутника n, то сума всіх внутрішніх і сума всіх зовнішніх = 4d * n, а, отже, сума зовнішніх кутів = 4dn - 2d (n - 2) = 4dn - 2dn + 4d = 2dn + 4d = 2d (n + 2).
- Побудувати повний шестикутник. Скільки у нього сторін?
- Побудувати повний шестістороннік так, щоб у нього не було паралельних сторін. Скільки у нього вершин?
- Знайти загальну формулу для числа сторін повного n-кутника і для числа вершин повного n-прихильника (вважаючи, що в нього немає паралельних сторін).
- Скільки діагоналей можна побудувати з однієї вершини простого n-кутника?
- Скільки всього діагоналей у простого n-кутника?
- Висловити в частинах прямого кута кожен внутрішній кут опуклого п'ятикутника, якщо у нього всі кути рівні між собою.
- Висловити для п'ятикутника попередньої задачі кожен зовнішній кут в частинах прямого кута.
- У трикутник кожен кут при підставі = ¾d. Знайти (в частинах прямого кута) його кут при вершині.
- У трикутник кут при вершині = 5/8 d. Знайти його кут при підставі.
- В опуклому чотирикутнику протилежні кути попарно рівні між собою. З'ясувати, що такий чотирикутник є паралелограм.