А тепер давайте розглянемо реалізацію черзі на основі масиву. Як і раніше, для простоти скористаємося масивом TList. По крайней мере, в цьому випадку нам не доведеться турбуватися про розподіл пам'яті та збільшенні розміру масиву.
Знаючи, як реалізується чергу на основі зв'язного списку, першим бажанням може бути, для імітації операції постановки в чергу, додавати елементи в кінець примірника масиву TList за допомогою методу Add, а для імітації зняття з черги - видаляти перший елемент за допомогою методу метод Delete ( або навпаки, вставляти в початок масиву, а видаляти з кінця). Проте, давайте подивимося, що при цьому буде відбуватися з масивом. При виконанні методу Add нічого цікавого не відбувається, за винятком тих випадків, коли доводиться збільшувати розмір масиву. Це операція класу O (l) - як раз те, що потрібно. Що ж стосується Delete, то тут все не так безхмарно. Для реалізації операції зняття з черги з масиву TList потрібно видалити перший елемент, що призведе до того, що всі елементи масиву перемістяться на одну позицію вперед. Така операція залежить від кількості елементів в масиві, тобто належить до класу 0 (п). Ось і дочекалися поганих новин. Ми не можемо поміняти місцями операції постановки в чергу і зняття з черги, тобто ми додаємо лише в початок списку і видаляємо з його кінця. Іншими словами, ми все одно отримуємо операцію класу 0 (п) при додаванні в початок списку.
У деяких джерелах описаний принцип все ж використовується для реалізації черги. Більш того, клас TQueue в модулі Contnrs, можливо, заснований на такому принципі.
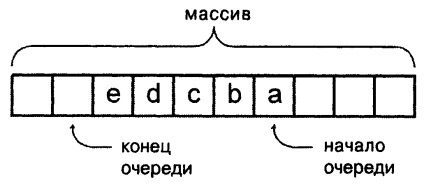
Малюнок 3.10. Використання масиву для організації черги
Яким чином можна реалізувати чергу на основі масиву, щоб обидві базових операції належали до класу 0 (1)?
Рішення полягає в використанні кільцевої черзі. Уявіть собі приймальню у стоматолога. Як правило, це кімната зі стільцями попід стінами. На відміну від черги в супермаркеті, де ви підходите до початку черги, штовхаючи візок, в приймальні ви сидите на стільці. При виклику чергового пацієнта все решта не встають і не переходять на сусідній стілець. Просто початок черги - якийсь важко зрозумілий атрибут (ага, таке враження, що в Америці немає черг до стоматолога.) - переходить до іншої людини. При виклику пацієнта цей атрибут передається наступному пацієнтові, і він стає "початком" черги. Таким чином, ніхто не встає зі стільців, просто деяким чином (можливо, за допомогою асистента стоматолога) визначається перший пацієнт в черзі. Подібного роду організація називається круговою чергою.
Для реалізації кругової черзі на основі масиву введемо змінну, яка буде містити індекс першого елемента в черзі. Крім того, введемо ще одну змінну, яка буде вказувати на кінець черги. Почнемо з масиву з деяким певною кількістю елементів (розмір будемо визначати на основі максимально можливої кількості елементів в черзі) і встановимо індекс початкового елемента рівним індексу кінцевого елемента. Фактично, це рівність означає, що черга порожня.
Постановка елемента в чергу еквівалентна установці значення елемента, на який вказує індекс кінця черги, рівним значенню записується в чергу елемента. Після цього значення індексу кінця черги потрібно збільшити на 1. Якщо після збільшення індексу він буде перевищувати розмір масиву, необхідно встановити його рівним 0, тобто індексом першого елементної.
Зняття елемента з черги означає повернення значення елемента, на який вказує індекс початку черги. Після цього значення індексу початку черги збільшується на 1. Якщо після збільшення індексу він буде перевищувати розмір масиву, встановити його рівним 0. Очевидно, що перед зняттям елемента з черги необхідно переконатися, що черга не порожня. Для цього слід перевірити, чи рівні індекси початку і кінця черги (в разі рівності індексів, чергу порожня).
І нам залишилося розглянути ще одну проблему: при постановці елемента в чергу необхідно переконатися, що нове значення індексу кінця черги не дорівнює значенню індексу початку черги. Якщо рівність дотримується, значить, все повністю заповнена елементами. На жаль, така ситуація також означає (по крайней мере, для процедури зняття з черги), що черга порожня. Таким чином, якщо така досить абсурдна ситуація виникає - порожня чергу еквівалентна заповненої - необхідно збільшити розмір масиву, переміщаючи всі наявні в масиві елементи і змінюючи значення індексів початку і кінця черги.
Інтерфейс класу TtdArrayQueue виглядає точно так само, як і інтерфейс класу TtdQueue.
Лістинг 3.31. клас TtdArrayQueue
Конструктор і деструктор мало чим відрізняються від відповідних методів класу TtdArrayStack.
Лістинг 3.32. Конструктор і деструктор класу TtdArrayQueue
Найцікавіше відбувається в методах Enqueue і Dequeue.
Лістинг 3.33. Методи Enqueue і Dequeue класу TtdArrayQueue
Як бачите, зняття елемента з черги включає повернення елемента, що знаходиться в позиції з індексом початку черги, а потім збільшення індексу на 1. Постановка в чергу включає запис елемента в позицію з індексом кінця черги і збільшення індексу на 1. Якщо кінець черги досягає її початку , розмір масиву збільшується за допомогою методу aqGrow:
Лістинг 3.34. Розширення розміру екземпляра класу TtdArrayQueue
Наведений метод є найбільш складним методом у всьому класі. При його виклику чергу заповнена, індекс кінця черги тимчасово дорівнює індексу початку (не забувайте, що це також означає, що черга порожня), причому необхідно збільшити розмір масиву TList. Перше, що ми робимо, - збільшуємо розмір масиву на 50%. Після цього потрібно виправити кільцеву чергу таким чином, щоб вона правильно враховувала вільне місце. Якщо значення індексу початку черги дорівнює 0, кільцева чергу була кругової, та все що потрібно зробити - змінити значення індексу кінця черги. Якщо ж значення індексу початку не дорівнює 0, черга була "закольцована" всередині масиву. Щоб переходити за елементами в правильному порядку, ми починаємо з індексу початку черги, доходимо до старого кінця масиву, переходимо до початку масиву і йдемо до індексу кінця черги (який дорівнює індексу початку черги). Тепер у нас є додаткові елементи, які знаходяться між старим і новим кінцем масиву. Отже, ми повинні помістити елементи, що знаходяться між початком черзі і старим кінцем масиву таким чином, щоб вони займали місце до нового кінця масиву. Після цього ми отримаємо правильний порядок елементів в кільцевої черзі.
Повний код класу TtdArrayQueue можна знайти на Web-сайті видавництва, в розділі матеріалів. Після вивантаження матеріалів знайдете серед них файл TDStkQue.pas.