В умовах ринкової системи управління виробничою і збутовою діяльністю підприємств і фірм в основі прийняття господарських рішень лежить ринкова інформація, а обгрунтованість рішень перевіряється ринком у ході реалізації товарів і послуг. При такому підході початковим пунктом всього циклу підприємницької діяльності стає вивчення споживчого попиту. Розглянемо деякі питання моделювання попиту і споживання.
Рівень задоволення матеріальних потреб суспільства (рівень споживання) можна виразити цільової функцією споживання U = U (Y), де вектор змінних Y> 0 включає різноманітні види товарів і послуг. Ряд властивостей цієї функції зручно вивчати, використовуючи геометричну інтерпретацію рівнянь U (Y) = С, де С - мінливий параметр, що характеризує значення (рівень) цільової функції споживання; в якості величини С може виступати, наприклад, дохід або рівень матеріального добробуту.
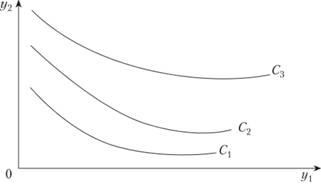
У просторі споживчих благ кожному рівняння U (Y) = С відповідає певна поверхню рівноцінних, або байдужих, наборів благ, яка називається поверхнею байдужості. Для наочності розглянемо простір двох благ, наприклад, у вигляді двох агрегованих груп товарів: продукти харчування (y1) і непродовольчі товари, включаючи послуги (y2) Тоді рівні цільової функції споживання можна зобразити на площині у вигляді кривих байдужості, що відповідають різним значенням С (рис . 8.1, де С1 <С2 <С3).
Будемо далі користуватися терміном "криві байдужості" незалежно від розмірності простору споживчих благ (кількості груп товарів).
З основних властивостей цільової функції споживання відзначимо наступні:
- функція U (Y) є зростаючою функцією всіх своїх аргументів, тобто збільшення споживання будь-якого блага при незмінному рівні споживання всіх інших благ збільшує значення даної функції. Тому більш віддалена від початку координат крива байдужості відповідає більшому значенню цільової функції споживання, а сам процес максимізації цієї функції на деякому обмеженому безлічі допустимих векторів Y можна інтерпретувати як знаходження допустимої точки, що належить кривій байдужості, максимально віддаленої від початку координат;
-
- криві байдужості не можуть перетинатися, тобто через одну точку простору благ (товарів, послуг) можна провести тільки одну поверхню байдужості. В іншому випадку один і той же набір благ одночасно відповідав би декільком різним рівням матеріального добробуту;
- криві байдужості мають негативний нахил до кожної осі координат, при цьому абсолютний нахил кривих зменшується при русі в позитивному напрямку по кожній осі, тобто криві байдужості є опуклими кривими.
Методи побудови цільової функції споживання засновані на узагальненні досвіду поведінки споживачів і тенденцій купівельного попиту в залежності від рівня добробуту. Як приклад наведемо квадратичную цільову функцію споживання для трьох агрегованих груп товарів, побудовану на основі обробки даних бюджетної статистики:
параметр а означає число дітей в сім'ї;
в1 - споживання продуктів харчування;
у2 - споживання промислових товарів;
у3 - споживання платних послуг (у вартісному вираженні).
Перейдемо до питання моделювання поведінки споживачів в умовах товарно-грошових відносин на базі цільової функції споживання. В основі моделі поведінки споживачів лежить гіпотеза, що споживачі, здійснюючи вибір товарів при встановлених цінах і наявному доході, прагнуть максимізувати рівень задоволення своїх потреб.
Нехай в просторі п видів товарів досліджується поведінка сукупності споживачів. Позначимо попит споживачів через вектор Y = (у1, у2, ..., уn), а ціни на різні товари - через вектор Р = (p1, р2, ..., рn). При величині доходу D споживачі можуть вибирати тільки такі комбінації товарів, які задовольняють бюджетному обмеженню. Припустимо, що перевагу споживачів на безлічі товарів виражається цільовою функцією споживання U (Y). Тоді найпростіша модель поведінки споживачів в векторній формі записи матиме вигляд:
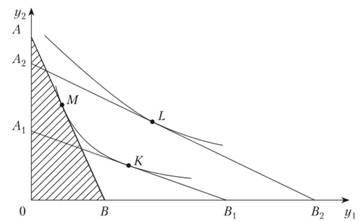
Геометрична інтерпретація моделі (8.1) для двох агрегованих груп товарів представлена на рис. 8.2.
Лінія АВ (в інших варіантах А1В1, А2В2) відповідає бюджетному обмеженню і називається бюджетною лінією (див. Докладніше в параграфі 8.2). Вибір споживачів обмежений трикутником АОВ (А1ОВ1, А2ОВ2). Набір товарів М, відповідний точці дотику прямої АВ з найбільш віддаленій кривої байдужості, є оптимальним рішенням (в інших варіантах це точки К і L). Легко помітити, що лінії АВ і А1В1 відповідають одному і тому ж розміру доходу та різними цінами на товари у1 і у2; лінія А2В2 відповідає більшому розміру доходу.
Спираючись на деякі висновки теорії нелінійного програмування, можна визначити математичні умови оптимальності рішень для моделі (8.1). Із завданням нелінійного програмування зв'язується так звана функція Лагранжа, яка для завдання (8.1) має вигляд
де множник Лагранжа l є оптимальною оцінкою доходу.
Позначимо приватні похідні функції U (Y) через. Ці похідні інтерпретуються як граничні корисні ефекти (граничні корисності) відповідних споживчих благ і характеризують приріст цільової функції споживання при збільшенні використання i-го блага (товару) на деяку умовну "малу одиницю".
Необхідними умовами того, що вектор Y 0 буде оптимальним рішенням, є умови Куна - Таккера:
. якщо (товар купується),
. якщо (товар не купується), (8.2)
Останнє з співвідношень (8.2) відповідає повному використанню доходу, і для цього випадку очевидно нерівність # 955; 0> 0. З умов оптимальності (8.2) випливає, що
Це означає, що споживачі повинні вибирати товари таким чином, щоб відношення граничної корисності до піні товару було однаковим для всіх придбаних товарів. Іншими словами, в оптимальному наборі граничні корисності обираних товарів повинні бути пропорційні цепам.