Нехай дифференцируема в точці x. За визначенням похідної. По теоремі про зв'язок межі з нескінченно малою. де при. Помножимо обидві частини на # 8710; x:
(1), де # 8710; x → 0,. .
Порівняємо ці нескінченно малі:
Якщо. то і # 8710; x - б.м. одного порядку
2) - б.м. більш високого порядку малості, ніж # 8710; x.
Отже, приріст функції # 8710; y складається з 2 x доданків: перше є головна частина приросту функції. лінійна щодо # 8710; x; а другий доданок - нескінченно мала вищого порядку малості, ніж # 8710; x.
Визначення. Диференціалом функції в точці x називається твір похідною в цій точці на приріст аргументу # 8710; x.
Знайдемо диференціал функції. Оскільки . то. тобто . (3)
Диференціал dx незалежної змінної x збігається з приростом # 8710; x.
Формула (2) з урахуванням (3) набуде вигляду: (4) - диференціал функції.
Значить - (позначення Лейбніца).
Похідну функції можна розглядати як відношення диференціала функції до диференціала незалежної змінної.
§13. Геометричний сенс диференціала.
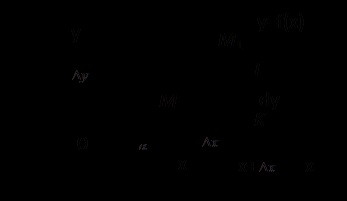
До графіка функції в точці M (x, y) проведемо дотичну.
# 945; - кут нахилу дотичній до осі Ox.
Дамо x прирощення # 8710; x. тоді функція одержить збільшення # 8710; y. На кривій отримаємо точку M1 (x + # 8710; x, y + # 8710; y), KT - приріст ординати дотичної.
|
Диференціал функції в т. X дорівнює збільшенню ординати дотичної при переході з точки з абсцисою x в точку з абсцисою x + # 8710; x.
Інваріантність форми диференціала (незалежність форми запису диференціала).
1) Нехай. x - незалежна змінна
2) Нехай. x = x (t) - функція від t.
- складна функція, x - проміжний аргумент.
(За правилом диференціювання складної функції)
У формулах (1) і (2) форма запису диференціала однакова. Властивість диференціала мати одну і ту ж форму записи незалежно від того чи є x незалежної змінною чи функцією іншої змінної називають инвариантностью форми диференціала.