Переглядаючи форум, я натрапив на своє повідомлення більш ніж 8-річної давності. У повідомленні я задавав громадськості питання, який, в общем-то, зводився до проблеми диференціювання матриці по вектору. На момент написання даної замітки, відповідь я так і не отримав. У той же час, зараз я не бачу принципових труднощів у цьому завданні.
Проблема в частій для технічних ВНЗ-ів ситуації: на першому курсі тобі розповідають про фізичні явища, для опису яких необхідне розуміння ротора. градієнта. дивергенції. а що це за оператори і як ними користуватися - розкажуть на другому курсі.
На перший погляд нічого незрозуміло: оператор диференціювання застосовується до матриць, деякі з яких ще й транспонувати, диференціювання відбувається по вектору і т.п. Але не варто панікувати: є правила для обчислення похідної і від сліду матриці, і від детермінанта твори матриць або логарифма детермінанта матриці - в нашому (форумном) випадку все досить просто.
Спершу опишемо загальні правила диференціювання при роботі з подібними об'єктами.
Похідна вектора по скаляру - вектор тієї ж розмірності, що складається з похідних відповідних елементів
Похідна скалярної функції f від векторного аргументу x - вектор тієї ж розмірності, що і x. рівний
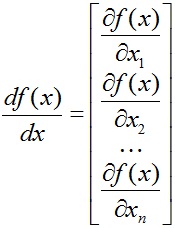
(Тобто вектор, складений з приватних похідних f за елементами вектора x.)
Похідна векторної функції g розмірності m по векторному аргументу x розмірності n - матриця розміром m × n. в якій перший рядок складається з приватних похідних елемента g1 за елементами вектора x і т.д .:
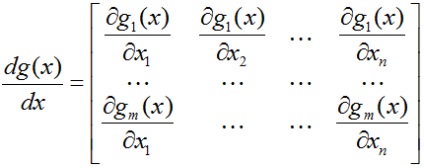
Наступні два результату з лінійної алгебри можна отримати, акуратно виконавши диференціювання за правилами, розглянутим раніше. Ці формули часто використовуються, тому випишемо і їх:
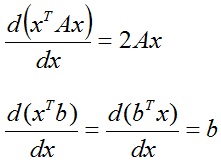
Власне, повертаючись до початкової проблеми (питання на форумі):
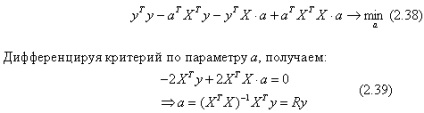
Як продифференцировать (2.38) і отримати (2.39)?
Розглянемо похідні доданків з (2.38).
Для першого - все очевидно з самого сенсу похідної:
Другий доданок (тут скористаємося однією з готових формул, описаних раніше):
Третє складова (скористаємося тією ж готової формулою, але попередньо трохи "доопрацюємо" вираз):
Якщо Ви не зрозуміли "перетворення" вище - ще раз детальніше:
Тут ми скористалися властивостями транспонування матриць:
Транспоновану твір матриць дорівнює добутку транспонованих матриць, взятих в зворотному порядку.
[. ]
Двічі транспонована матриця А дорівнює вихідній матриці А.
За допомогою цих властивостей ми здійснили перетворення, що зводять вираз до виду, зручного для застосування готової формули.
Четверте доданок (скористаємося інший готової формулою):
Зберемо все воєдино і згрупуємо доданки:
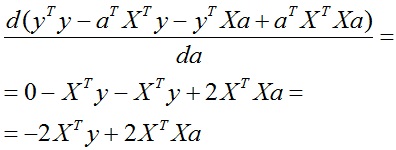
Саме такий результат ми отримали в (2.39).